P01 - Prädiktorfunktion
Die Datenmodellierung
Ein wichtiger Beitrag des Teilprojekts P01 zum Sonderforschungsbereich P01 besteht in der Datenmodellierung der experimentellen Datensätze. Hierfür ist eine zentrale Dateninfrastruktur notwendig, welche ein globales Datenmodell für alle durchgeführten Urformung- und Einfärbungsprozesse sowie Deskriptorermittlungen (sog. Prozessschritte) umfasst. Um eine Rekonstruierbarkeit einzelner Experimente im Sinne einer guten wissenschaftlichen Praxis zu gewährleisten, ist eine individuelle formale Spezifikation eines jeden Prozesses notwendig. Die Menge aller Prozesse umfasst dabei alle urformenden und einfärbenden Prozesse sowie die Deskriptor- und Werkstoffeigenschaftsermittlungen. Es werden hierbei nicht nur die experimentellen Daten selbst, sondern ebenfalls die Rohdaten und die Prozessparameter (Versuchsparameter) erfasst. Für die formale Spezifikation ist eine Bibliothek auf Basis der gängigen JavaScript Object Notation (JSON) entwickelt worden, die eine gute Lesbarkeit ermöglicht und gleichzeitig nativ vom Dateneingabesystem verarbeitet werden kann.
Diese Spezifikation definiert den Datentyp oder den Wertebereich jedes einzelnen Prozessparameters, wodurch eine Konsistenzprüfung direkt bei der Eingabe erfolgen kann. Eine weitere, wichtige Funktionalität besteht in der Implementierung von Einleseroutinen (engl. Parser), die funktional das Einlesen, die Aufbereitung und die strukturierte Ablage von Forschungsdaten realisieren.
Auf Basis der formalen Spezifikationen werden vom eigens implementierten web-basierten Eingabesystem individuelle Eingabemasken generiert, die von den jeweiligen wissenschaftlichen Mitarbeiter*innen bzw. Techniker*innen zur Eintragung der Experimente in die zentrale Datenbank verwendet werden. Das Eingabesystem implementiert hierbei ein rollenbasiertes Nutzermodell, wodurch die Schreibrechte entsprechend restriktiv vergeben werden können und eine Nachvollziehbarkeit im Sinne der Data Provenance gewährleistet wird. Zudem wird eine Verbindlichkeit zwischen dem Autor und den Datensätzen erzeugt.
Zusätzlich ist ein Konzept zur Versionierung der Prozessspezifikationen entworfen worden, um die Evolution der einzelnen Prozesse zu adressieren. Während der ersten Förderphase wurden insgesamt 60 Prozesse spezifiziert, aus denen kumuliert 380 Versionen resultierten. Diese Spezifikationen wurden in gemeinsamen Experteninterviews in enger Kooperation mit dem Arbeitskreis „Datenaustausch und Datenmanagement“ durchgeführt. Bei der Datenmodellierung und dem Entwurf der Schnittstellen nahmen die FAIR-Prinzipien eine wichtige Stellung ein.
Die Datenbank
Entgegen der weiten Verbreitung von SQL-basierten Datenbanken, wurde bewusst eine dokumentorientierte Datenbank verwendet. Ein klassisches SQL-Datenbanksystem besitzt eine vorgegebene Tabellenstruktur, die bei komplexen Anfragen typischerweise umfangreiche Vereinigungsoperationen (sog. JOINs) erfordert. Diese Operationen bilden oftmals einen massiven Engpass bei großen Datensätzen. Ist hingegen der kausale Zusammenhang und die spätere semantische Verwendung a-priori gegeben, können alle kohärenten Teile der Information direkt in einem einzelnen Dokument gespeichert und in der dokumentorientierten Datenbank abgelegt werden.
Dieser semantische Datenzusammenhang ist im Sonderforschungsbereich 1232 bekannt, da die Untersuchungen strikt probenorientiert durchgeführt und die Resultate jedes Prozesses als atomare Einheit interpretiert werden können. Hierbei werden die Proben selbst mittels eines neu entwickelten, standardisierten Schemas benannt, wodurch die einzelnen Proben inkl. ihrer gesamten Prozesshistorie auch im Fortlauf des Projekts direkt adressierbar sein werden. Die Verwendung dieser probenorientierten Ablage in Kombination mit dem dokumentenorientierten Datenbanksystem eliminiert die Notwendigkeit ganzheitlicher Vereinigungen und reduziert die Anzahl von Verknüpfungen in der Datenablage bzw. beim Datenzugriff massiv. Generell eignet sich eine dokumentenorientierte Datenbank ideal für heterogene Datensätze, da keine feste Tabellenstruktur vorgegeben ist, die rückwirkend angepasst werden müsste.
Bei dem entwickelten, dokumentenorientierten Datenmodell wurden zwei unterschiedliche Klassen eingesetzt: Die erste Klasse modelliert einen atomaren Prozessschritt inkl. aller assoziierten Meta-Informationen, Prozessparameter und Messdaten. Die zweite Klasse modelliert eine Probe als Entität im System, beinhaltet zentrale Attribute, beispielsweise die eindeutige Proben-ID, und bildet ferner die Prozesshistorie in Form einer linearen Datenstruktur (engl. Array) ab. Dieses Array besteht aus einer chronologisch geordneten Sequenz von Prozessschritten, wobei die jeweiligen Prozessschritte nur als Referenz hinterlegt werden. Insbesondere thermische Einfärbungsprozesse sowie Urformungsprozesse (auf der Mikroebene) werden gleichzeitig auf eine Vielzahl von Proben angewendet. Die Verwendung von Referenzen erlaubt es, dass die Parameter dieser o.g. Prozesse nur einfach gespeichert werden müssen, wodurch eine Datendeduplikation erzielt werden kann. Außerdem ermöglicht diese Struktur die Unterscheidung zwischen invasiven und nicht-invasiven Prozessen: Sofern der Zustand einer Probe durch einen Prozessschritt modifiziert (eingefärbt) wird, entsteht eine neue (virtuelle) Einrückung und alle nachfolgenden Prozessschritte sind mit diesem veränderten Zustand assoziiert. Dieses Modell ermöglicht es, auf alle Datensätze, die mit einer Einzelprobe oder einem spezifischen Probezustand verbunden sind, einfach zuzugreifen.
Als zentrale Datenbank wird die MongoDB (vgl. https://www.mongodb.com) genutzt, die sich insbesondere durch eine gute Konnektivität bzgl. einer Vielzahl von relevanten Programmiersprachen auszeichnet. Ein weiterer, wichtiger Aspekt bestand in einer effizienten Ablage der Dokumente selbst, bspw. durch eine Datendeduplikation, die durch MongoDB ermöglicht wird.
Es sind neue Basisoperatoren für den applikationsspezifischen Datenzugriff entwickelt und den anderen Teilprojekten als Softwarebibliothek zur Verfügung gestellt worden. Die Erweiterbarkeit des nativen Befehlssatzes von MongoDB wurde dazu verwendet, ein Query-Framework direkt in die Datenbank zu integrieren, welches die benötigten Funktionalitäten bzgl. der Datenabfrage bereitstellt. Diese Basisoperatoren berücksichtigen, neben den Proben- und Prozessdaten, ebenfalls die Informationen aus der formalen Spezifikation der einzelnen Prozesse.
Mehr Informationen zu der Arbeit mir der Datenbank finden Sie auf folgenden Links:
BigData-Insider: Bremen geht neue Wege in der Materialforschung
Das Expertenwissen
Zusätzlich wird in den Basisoperatoren weiteres Wissen über die Korrelationen - sowohl auf einer groben (Prozessebene) Granularität als auch feinen (Ebene der charakteristischen Werten) Granularität - verwendet. Diese Korrelationen werden mathematisch in Form von Adjazenzmatrizen repräsentiert. Hierbei beschreiben die Matrizen sowohl wichtige Korrelationen für die Skalierungsfunktion als auch welche für die Übertragungsfunktion. Zum Zwecke des zentralen Zugriffes werden diese ebenfalls in der Datenbank abgelegt.
Die Einführung dieser Matrizen ist dadurch begründet, dass der zur Verfügung stehende Datenumfang, der einzelne Stützstellen beschreibt, wesentlich geringer ausgefallen ist als ursprünglich angenommen. Außerdem war die zu betrachtende Dimensionalität signifikant höher als angenommen, welches sich aus den konkreten Ermittlungsverfahren der charakteristischen Werte aus den deskriptorermittelnden Prozessen ergeben hat. Die einzelnen Dimensionen sind somit aus Datensichtsicht dünn besetzt, welches insbesondere beim Einsatz von datengetriebenen Techniken problematisch ist - das sog. Sparse Data Problem. Durch diese zwei Gegebenheiten ist es nicht möglich, den hochdimensionalen Raum der charakteristischen Werte datengetrieben zu reduzieren bzw. einen Startpunkt zu wählen. Dies betrifft sowohl den Umfang der Stützstellen bzgl. verschiedener Legierungssysteme als auch die Variationen auf der Mikroebene im Hochdurchsatz.
Neben der reinen Ablage besitzt jede Adjazenzmatrix ebenfalls eine Versionsnummer, wodurch die Korrelationen adaptierbar sind. Dies kann beispielsweise durch neue, wissenschaftlich tiefe Erkenntnisse aus den jeweiligen Teilprojekten erfolgen oder durch algorithmisch rückgekoppelte Korrelationsanalysen, sobald eine ausreichende Datenbasis existiert. Der initiale Zustand der Matrizen wurde dabei durch umfangreiche Experteninterviews ermittelt und zuerst mittels tertiärer Logik innerhalb einer Gleitkommazahl, welche sich direkt verfeinern lässt, wie folgt kodiert: 0 → „keine Korrelation angenommen“, 0,5→ „Korrelation als möglich angenommen“ und 1,0 → „Korrelation angenommen“.
Eine Visualisierung dieser Matrizen ist in Abbildung 1 gezeigt.
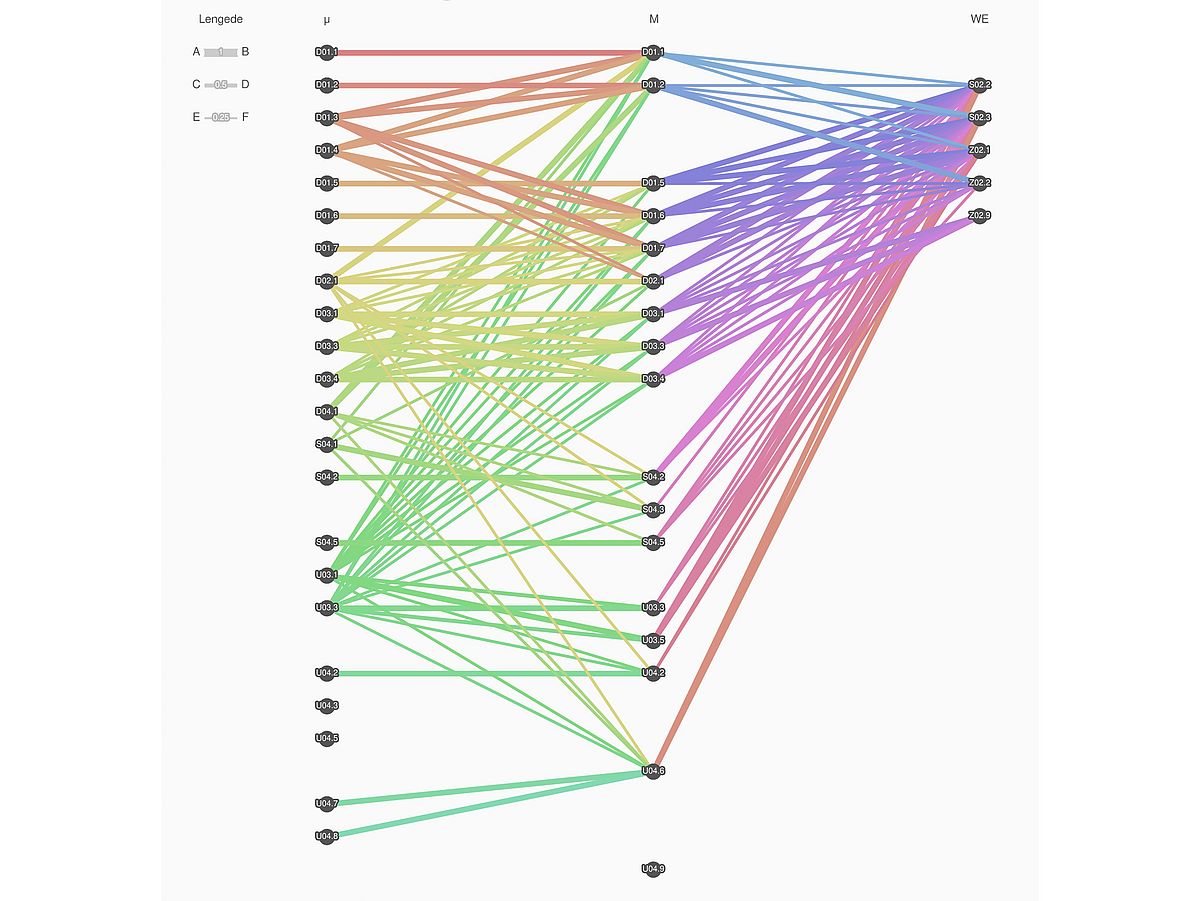
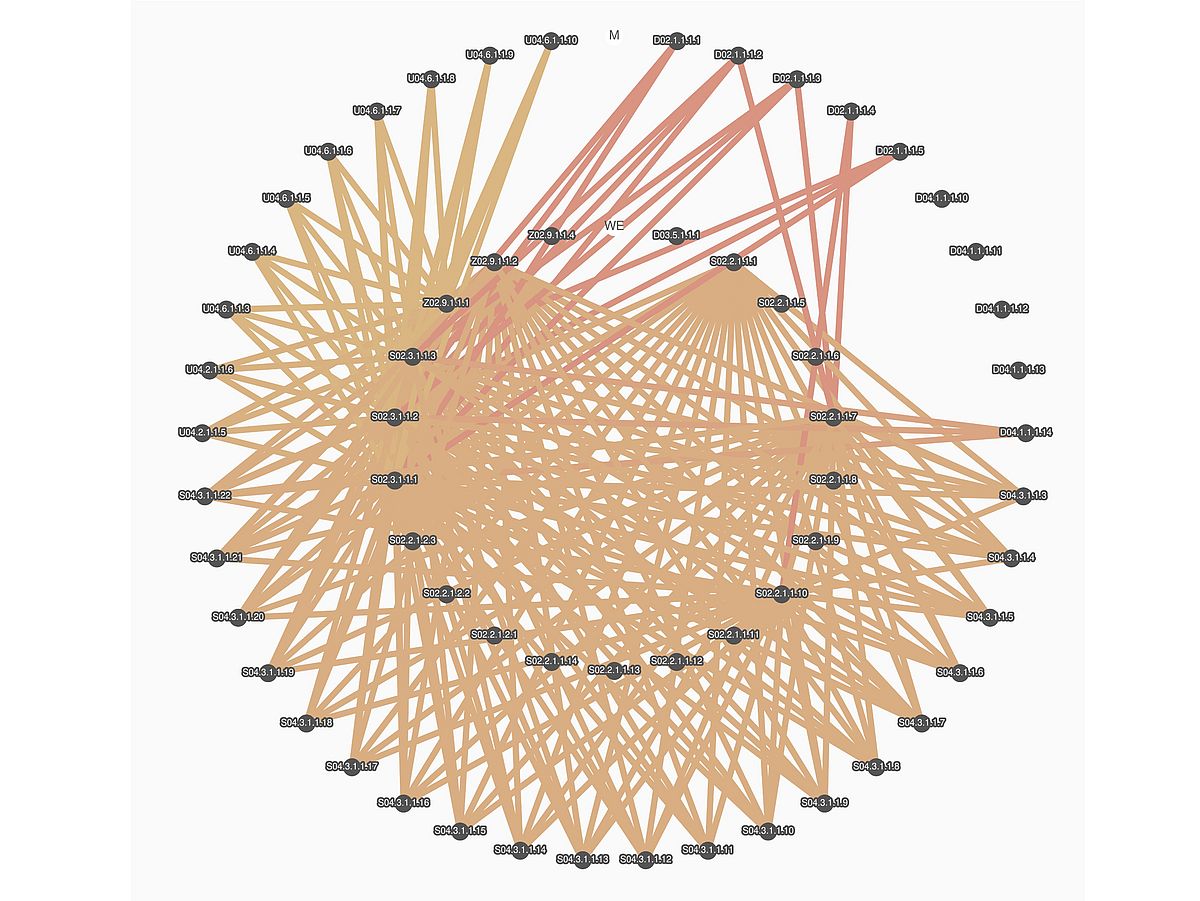
Durch die Kombination aus Datenbasis, Prozessspezifikation sowie Adjazenzmatrizen ist es mittels neu entwickelter Basisoperatoren möglich, Anfragen an die Datenbank zu stellen, welche beispielsweise spezifische Werkstoffkennzahlen eines standardisierten Zugversuches ausgeben, die bzgl. eines spezifischen charakteristischen Wertes eines Kugelstrahlversuches aus dem Teilprojekt U04 (Mechanisches Einfärben) auf der Mikroebene korrelieren. Diese Funktionalität bildet für die Prädiktorfunktion und die algorithmische Umsetzung des nachfolgend beschriebenen Hypothesensystems eine wichtige Grundlage.

Das Hypothesensystem
Ein Hypothesensystem in Kombination mit einer domänenspezifischen Sprache (DSL) ist entwickelt worden, welches es ermöglicht, Hypothesen über Eigenschaften der existierenden Datenbasis zu formulieren und zu evaluieren. Die Hypothesen bestehen zum einen aus Voraussetzungen (engl. Assumptions) und zum anderen aus Behauptungen (engl. Assertions).
Hierbei werden die Voraussetzungen dazu verwendet, einen Gültigkeitsbereich der Hypothesen zu definieren. Dies ermöglicht es beispielsweise, die in der Hypothese nachfolgenden Behauptungen nur auf eine spezifische Probengeometrie oder Wärmebehandlung anzuwenden. Es können auch weitere, komplexere Eigenschaften beschrieben werden, die sich auf Informationen über aktuelle Korrelationen (aus den Adjanzenzmatrizen) beziehen, wofür Modellierungstechniken aus dem Bereich des Model-Checking verwendet wurden.
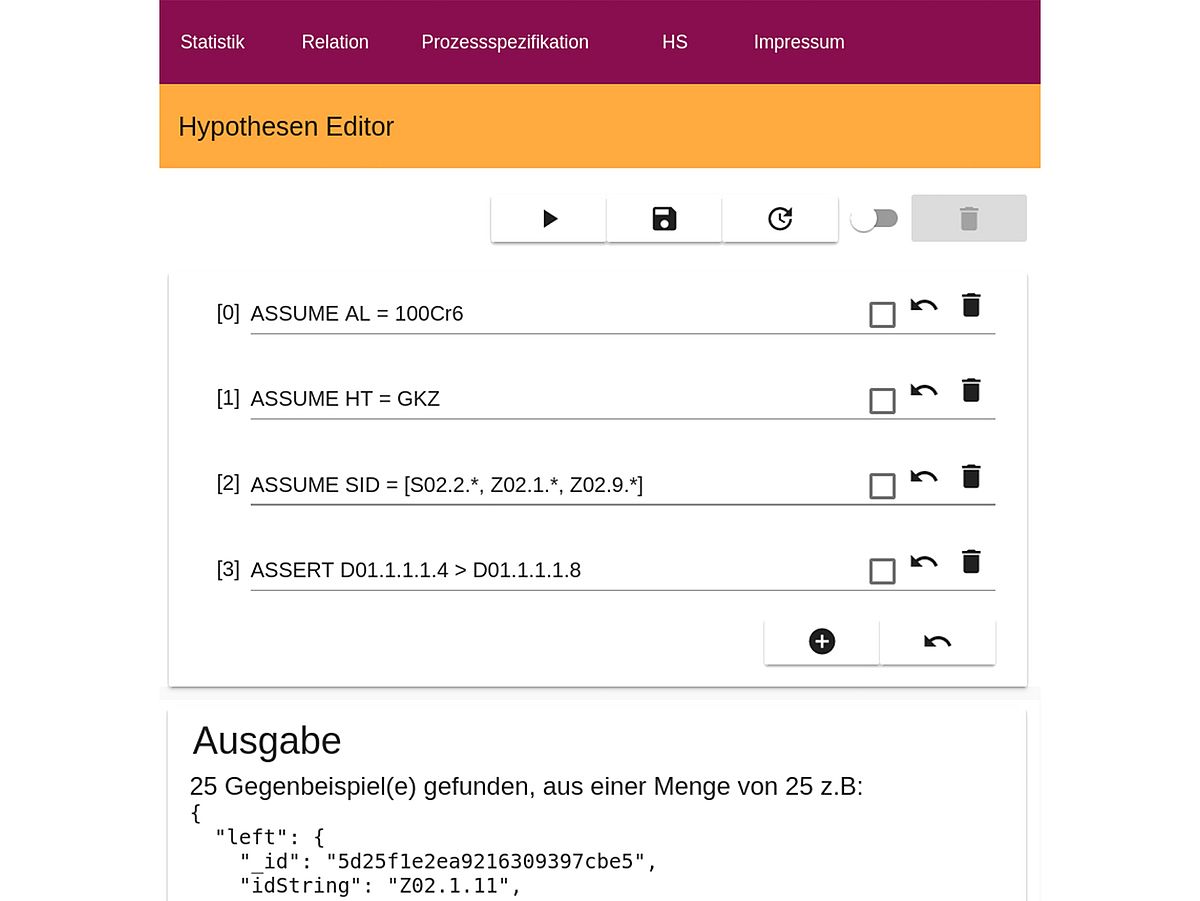
Abbildung 2 zeigt den web-basierten Hypothesen-Editor zur Formulierung neuer Hypothesen, die im Back-End evaluiert werden. Abbildung 3 zeigt die unterstützten Sprachkonstrukte der entwickelten DSL, um sowohl mehrstufige Voraussetzungen als auch Behauptungen zu beschreiben, die logisch miteinander verbunden sind. Zusätzlich werden die eingeführten Nomenklaturen bzgl. der Proben- und Prozessbezeichnung sowie der Bezeichnung eines einzelnen charakteristischen Wertes unterstützt. Es sind die gängigen arithmetischen Operatoren verfügbar, ebenfalls beim Vergleich mit Konstanten. Außerdem können komplexere Charakteristika auf den Datenreihen berechnet werden, die beispielweise den Pearson’s Korrelationskoeffizienten (PCC) berechnen und einen Vergleich über diesen ermöglichen.
Die formulierten Hypothesen können durch das entwickelte System validiert bzw. falsifiziert werden. Im Falle der Falsifikation werden entsprechende Gegenbeispiele aufgezeigt, d.h. Datenartefakte, für die die skizzierten Behauptungen nicht gültig sind, und die somit die Hypothese widerlegen. Eine Validation impliziert, dass die formulierte Hypothese für die gesamte Datenbasis unter den Voraussetzungen (Assumptions) gültig ist.
Die Prädiktorfunktion
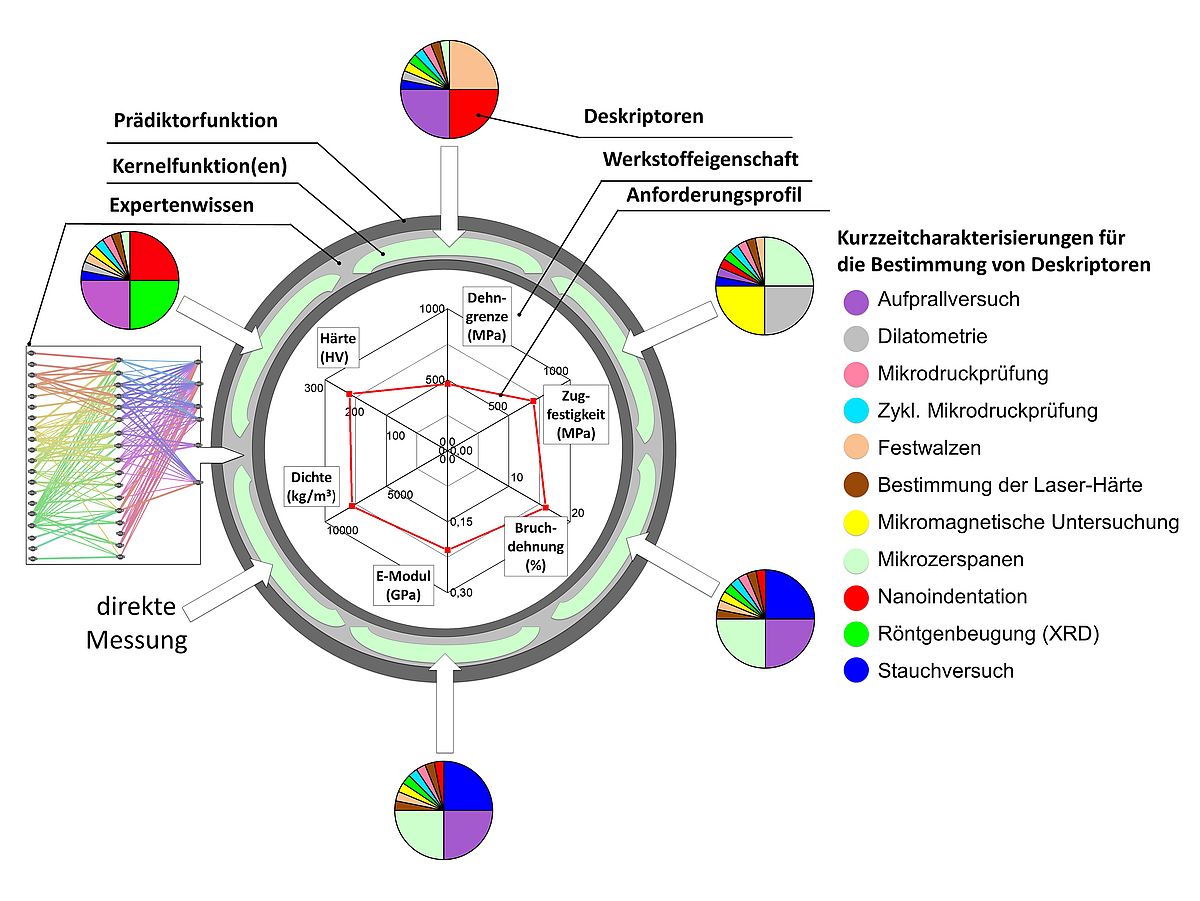
Die entwickelte Prädiktorfunktion bildet einen wesentlichen Aspekt der Gesamtmethode und ist stark in den gesamten Datenfluss eingebunden. Die Prädiktorfunktion ermöglicht eine Vorhersage der Zusammenhänge zwischen den ermittelten Deskriptoren auf der Mikroebene und den Werkstoffeigenschaften der korrelierten Makroproben. Zum Aufbau der Prädiktorfunktion werden Stützstellen benötigt, die sich (a) aus korrelierten Deskriptorermittlungen auf Mikro- und Makroebene und (b) aus korrelierten Deskriptoren sowie Werkstoffeigenschaften auf Makroebene zusammensetzen. Hierbei werden die Datensätze (a) für die Konstruktion der Skalierungsfunktion verwendet, welche die Skaleneffekte zwischen der Mikro- und Makroebene abbildet.
Die Datensätze (b) werden zur Konstruktion der Übertragungsfunktion genutzt, welche die eigentliche Vorhersage von Werkstoffeigenschaften realisiert.
Die Prädiktorfunktion besteht aus funktionaler Sicht aus einer Komposition dieser beiden Funktionen und wurde auf der 10. IEEE Symposium Series on Computational Intelligence (IEEE SSCI 2017) publiziert.
Für die Stützstellen sind hierbei zum einen das verwendete Legierungssystem, dessen Untersuchung sich in der ersten Förderphase auf die Legierung 100Cr6 konzentriert hat, und zum anderen die Wärmebehandlungen elementar. Die Wärmebehandlung muss hierbei derart erfolgen, dass vergleichbare Mikrostrukturen entstehen. Die notwendigen Parameter hierfür wurden im Arbeitskreis (Skalierung) bestimmt, in Form eines Variantenplans spezifiziert und mit in die Prozessspezifikation aufgenommen.
Zusätzlich ist ein Zugriff auf die Adjazenzmatrizen notwendig, um einzelne sog. Kernelfunktionen zu erzeugen, welche jeweils zwei Eingabevektoren auf einen Wert abbilden, der das Skalarprodukt beider Vektoren repräsentiert. Jede Kernelfunktion ist gemäß des Expertenwissens für eine Teilmenge aller Deskriptoren und Werkstoffeigenschaften gültig. Diese Segmentierung war notwendig, um die hohe Dimensionalität und das Sparse Data Problem zu adressieren, und erfolgte auf Basis der initial erwarteten Korrelationen.
Je nach strukturellen Gegebenheiten der verwendeten Deskriptoren bzw. Werkstoffeigenschaften können unterschiedliche Kernelfunktionen und -parameter verwendet werden, die individuell zu ermitteln sind.
Eine Kernelfunktion wird instanziiert und im Anschluss mit den Datenpunkten der Stützstelle trainiert, die durch Einsatz der Basisoperatoren aus der Datenbasis extrahiert werden. Dabei sieht das Verfahren vor, dass nach Ermittlung weiterer Stützstellen das Training wiederholt wird. Hierbei ist zu berücksichtigen, dass die Kernelfunktion nach jedem Trainingsschritt einen spezifischen Zustand besitzt, der durch die berechnete Parametrierung definiert ist. Eine Kernelfunktion wird im entwickelten Framework nach jedem Training zugreifbar abgelegt. Die Prädiktorfunktion aggregiert, je nach erfolgter Eingabe für die Prädiktion, entsprechend der Ergebnisse aller Kernelfunktionen. Durch die Einführung von Kernelfunktionen ließ sich der sog. Kernel-Trick realisieren, der durch die Kombination mehrerer einfacher Regressionen ermöglicht, nicht-lineare Datensätze bestmöglich zu repräsentieren. Diese Methode wurde im SSCI Paper publiziert, wobei der Fokus auf Kernelfunktionen lag, die dem Typ der Kernel-Recursive Least-Mean-Square (KRLMS) Techniken entsprachen, die u.a. bei erneuten Trainingsschritten durch ihren rekursiven Charakter gute Prädiktionsergebnisse erzielt haben. Die Parameterwahl wurde dabei mittels Cross-Validation optimiert.
Publikationen
R. Drechsler, S. Huhn, Chr. Plump: Combining Machine Learning and Formal Techniques for Small Data Applications - A Framework to Explore New Structural Materials. Euromicro Conference on Digital System Design (DSD), Portorož, Slowenien, 2020, [Link zur Konferenz], [Link zum PDF]
S. E. Harshad Dhotre, Krishnendu Chakrabarty, Rolf Drechsler: Machine Learning-based Prediction of Test Power, IEEE European Test Symposium (ETS), Baden-Baden, Germany, 2019.
D. T. Sebastian Huhn, Rolf Drechsler: Hybrid Architecture for Embedded Test Compression to Process Rejected Test Patterns, IEEE European Test Symposium (ETS), Baden-Baden, Germany, 2019.
S. Huhn, D. Tille, R. Drechsler: A Hybrid Embedded Multichannel Test Compression Architecture for Low-Pin Count Test Environments in Safety-Critical Systems, International Test Conference in Asia (ITC-Asia), Tokyo, Japan, 2019.
B. Ustaoglu, S. Huhn, F. S. Torres, D. Große, R. Drechsler: SAT-Hard: A Learning-based Hardware SAT-Solver, EUROMICRO Digital System Design Conference (DSD), Kallithea - Chalkidiki, Greece, 2019.
M. Picklum, M. Beetz: MatCALO: Knowledge-enabled machine learning in materials science, Computational Materials Science 2019, 163, 50-62
Huhn, S., Frehse, S., Wille R., Drechsler, R. Determining Application-Specific Knowledge for Improving Robustness of Sequential Circuits. IEEE Transactions On Very Large Scale Integration (VLSI) Systems.
[Link zur Zeitschrift ] [Link zum Artikel]
Huhn, S., Eggersglüß, S., Drechsler, R. Enhanced Embedded Test Compression Technique for Processing Incompressible Test Patterns. 31. GI/GMM/ITG Testmethoden und Zuverlässigkeit von Schaltungen und Systemen. 2019. Prien am Chiemsee, Germany. [Link zum Workshop] [Link zum PDF]
Ustaoglu, B., Huhn , S., Große, D., Drechsler, R. SAT-Lancer: A Hardware SAT-Solver for Self-Verification. 28th ACM Great Lakes Symposium on VLSI (GLVLSI). 2018. Chicago, Illinois, USA. [Link zur Konferenz]
Huhn, S., Merten, M., Eggersglüß, S., Drechsler, R. A Codeword-based Compaction Technique for On-Chip Generated Debug Data Using Two-Stage Artificial Neural Networks. 30. GI/GMM/ITG Testmethoden und Zuverlässigkeit von Schaltungen und Systemen (TuZ 2018). 2018. Freiburg (Breisgau), Germany. [Link zum Workshop]
C. Große, C. Sobich, S. Huhn, M. Leuschner, R. Drechsler, L. Mädler: Arduinos in der Schule - Lernen mit Mikrocontrollern, Computer + Unterricht 2018.
Sebastian Huhn, Heike Sonnenberg, Stephan Eggersgluess, Brigitte Clausen, Rolf Drechsler. Revealing Properties of Structural Materials by Combining Regression-based Algorithms and Nano Indentation Measurements Conference. 10th IEEE Symposium Series on Computational Intelligence (SSCI), Hawaii, USA, 2017 [Link zur Konferenz] [Link zum PDF [PDF] (1.9 MB)]
Harshad Dhotre, Stephan Eggersglüß, Rolf Drechsler. Identification of Efficient Clustering Techniques for Test Power Activity on the Layout. 26th IEEE Asian Test Symposium (ATS), Taipei, Taiwan, 2017 [Link zur Konferenz]
Sebastian Huhn, Stephan Eggersglüß, Rolf Drechsler. Reconfigurable TAP Controllers with Embedded Compression for Large Test Data Volume. 30th IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT), Cambridge, UK, 2017 [Link zur Konferenz][Link zum PDF [PDF] (255 KB)]
Sebastian Huhn, Stephan Eggersglüß, Krishnendu Chakrabarty, Rolf Drechsler. Optimization of Retargeting for IEEE 1149.1 TAP Controllers with Embedded Compression. Design, Automation and Test in Europe (DATE), Lausanne, Schweiz, 2017 [Link zur Konferenz] [Link zum PDF [PDF] (285 KB)]
Drechsler, R., Eggersglüß, E., Ellendt, N., Huhn, S., Mädler, L. Exploring Superior Structural Materials Using Multi-Objective Optimization and Formal Techniques. 6th IEEE International Symposium on Embedded Computing & System Design (ISED), December 15-17, Patna, India, 2016.
Projektleitung
Prof.Dr. phil. nat.habil.
Rolf Drechsler
drechslerprotect me ?!informatik.uni-bremenprotect me ?!.de
assoziierte Projektleitung
Prof.
Michael Beetz, PhD
michael.beetzprotect me ?!uni-bremenprotect me ?!.de
Projektbearbeitung
Sebastian Huhn
huhnprotect me ?!informatik.uni-bremenprotect me ?!.de
Mareike Picklum
mareikepprotect me ?!cs.uni-bremenprotect me ?!.de

