Consistent approximations of the three-dimensional linear elasticity theory
Subject:
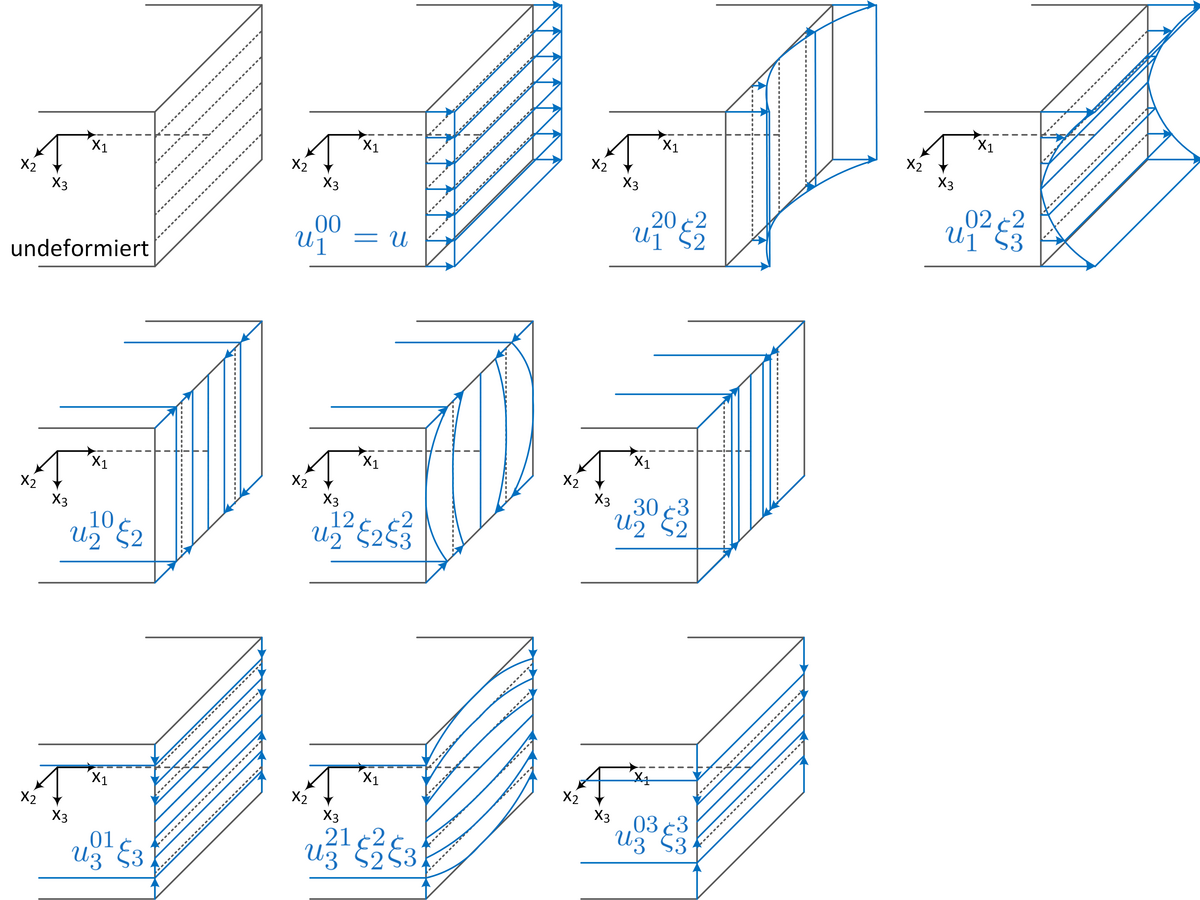
The 3D theory of linear elasticity is used to calculate structures (e.g. beams, supports) made of linear-elastic materials (e.g. metal, ceramic). This theory can be formulated as coupled, partial differential equations and can only be solved in closed form for a few special cases. A large number of closed solutions result from 2D and 1D approximations. The 2D case contains the plate and disk problem. In the 1D case, two beam problems, a rod problem and a shaft problem are identified.
Project duration:
01.09.2015 - 31.08.2020
Partners:
Institute for Lightweight Construction and Design (KLuB), Technische Universität (TU) Darmstadt
Project description:
Classically, both, i.e. the 2D and 1D, theories are derived via kinematic a-priori assumptions (cf. Bernoulli assumptions). Based on the consistent approach, the research project presented here does not require these assumptions. In this procedure, the elastic potentials of 3D theory are reduced to quasi 2D or 1D theories by series developments. The equivalence between these infinite number of equations and the 3D theory has already been proven. By means of the uniform approximation approach (decomposition by geometrical ratios) the infinite equations are finally transferred into solvable systems of equations.
The main focus of our research is on plate theory. Here, the so-called "Reissner" terms (edge effects) should ideally be integrated into the consistent theory. Furthermore, a method is developed to derive a differential equation for all displacement coefficients. In addition, these differential equations should satisfy the local conditions. Finally, plate theories with different material symmetries are investigated.