Projekte
Aktuelle Projekte
#MOIN – Modellregion Industriemathematik: Ein Transferprojekt für eine nachhaltige und selbsttragende Modellregion Industriemathematik
Das #MOIN-Projekt wird seit 2023 vom Bundesministerium für Bildung und Forschung (BMBF) als eine von deutschlandweit 12 T!-Raum-Initiativen gefördert, um TransferRäume für die Zukunft von Regionen entstehen zu lassen.
Projektzeitraum: Dezember 2023 – Dezember 2026
Projektbeteiligte (im Teilprojekt "Campus - Nachbarschaft - Sichtbarkeit"): Prof. Dr. Christine Knipping (Verbundkoordination, Universität Bremen – AG Mathematikdidaktische Unterrichtsforschung (AGMU)), Dr. Matthias Knauer (Verbundkoordination, Universität Bremen – AG Optimierung und Optimale Steuerung (AG O2C)), Luisa Gunia (Universität Bremen, AGMU), Nora Niesert (Universität Bremen, AG O2C), Bianka Hofmann (Fraunhofer MEVIS), Dr. Anna Rörich (Fraunhofer MEVIS), Rieke Alpers (Fraunhofer MEVIS)
Worum geht's?
Ziel des #MOIN-Projektes ist es, lebendige Mathematik in Schulen, Industrie, Politik und Gesellschaft zu bringen und zu zeigen, dass (Industrie-)Mathematik für alle zugänglich und voller Chancen ist. #MOIN verfolgt dabei einen ganzheitlichen Transferansatz und fokussiert sich auf die vier zentralen Bereiche #MATHWARE (Industriemathematik als Innovationstreiber in der Industrie), #MATHUP (Industriemathematik auf dem Weg ins Unternehmertum), #MATHDAYS (Industriemathematik in der Schule) und #MATHINSIDE (Industriemathematik in der Öffentlichkeit).
In dem Transferansatz #MATHDAYS geht es insbesondere darum, Jugendlichen und ihren Lehrkräften den Nutzen von Mathematik zu vermitteln. Dafür werden Aktivitäten, die auf dem Campus stattfinden, und Aktivitäten in der Nachbarschaft der Jugendlichen unterschieden. In diesen Aktivitäten sollen die regional vorhandenen wissenschaftlichen, wirtschaftlichen und gesellschaftlichen Innovationspotenziale erfahrbar und sichtbar gemacht werden, um Jugendliche, ihre Lehrkräfte und weitere soziale Akteure auf die Potenziale der Industriemathematik aufmerksam zu machen und ihre Sensibilität für dieses Potenzial zu erhöhen.
Der Baustein #MATHINSIDE wendet sich an die breitere Öffentlichkeit und hat es sich zum Ziel gesetzt, bestehende Verknüpfungen der Region mit unterschiedlichen Aspekten der Mathematik und Mathematikgeschichte herauszustellen und zu teilen. Dabei sollen auch neue Gedenkorte etabliert werden, um die (Industrie-)Mathematik als lebendige Disziplin zu vermitteln und die Sichtbarkeit der Mathematik in der Region aktiv zu beeinflussen.
Weitere Informationen finden Sie auf der Website des #MOIN-Projektes



Abgeschlossene Projekte
Digi-Spotlights – Ein Lehrkonzept zur Verzahnung und Vernetzung von fachwissenschaftlichen und fachdidaktischen Inhalten im Lehramtsstudium
Das Projekt Digi-Spotlights ist ein interdisziplinäres und fächerübergreifendes Teilprojekt des Gesamtprojekts "Schnittstellen gestalten" der Qualitätsoffensive Lehrerbildung, gefördert durch das Bundesministerium für Bildung und Forschung.
Projektzeitraum: Januar 2016 - Juni 2019 (1. Phase) und Juli 2019 - Dezember 2023 (2. Phase)
Projektbeteiligte: Prof. Dr. Angelika Bikner-Ahsbahs (Projektleitung 1. Phase, Mathematik), Prof. Dr. Marcus Callies (Englisch), Prof. Dr. Andreas Klee (Politik), Prof. Dr. Christine Knipping (Projektleitung 2. Phase, Mathematik), Dr. Fiene Bredow, Dr. Erik Hanke, Stefanie Hehner, Nelli Mehlmann, Nils Quentel, Dr. Ingolf Schäfer, DanielaSchansker, Dr. Hendrik Schröder
Worum geht's?
Während Studierende des Lehramts fachdidaktische Anteile im Studium aufgrund ihres unmittelbaren Bezugs zur Unterrichtspraxis häufig sehr begrüßen, erschließt sich vielen die Relevanz fachwissenschaftlicher Veranstaltungen für den Lehrberuf weniger. Auch Bezüge zwischen der Fachwissenschaft und anderen Studienanteilen wie der Fachdidaktik werden nicht immer erkannt.
In Digi-Spotlights werden innovative Lehrkonzepte (Spotlights) entwickelt und weiterentwickelt, die fachwissenschaftliche und fachdidaktische Elemente in der universitären Lehrerausbildung systematisch miteinander verzahnen. Diese Verzahnung wird im Hinblick auf die Vernetzung der beiden Inhaltsbereiche im Denken und Handeln Studierender untersucht.
In den (weiter)entwickelten Lehrkonzepten der drei Modellkonzepte in den Fächern Englisch, Mathematik und Politik werden fachwissenschaftliche Inhalte von den Studierenden didaktisch aufbereitet und in einem Unterrichtsversuch mit Schüler:innen praktisch erprobt.
Weitere Informationen finden Sie auf der Webseite des Projekts Digi-Spotlights.
Aktuelle Promotionsprojekte
Marie-Theres Brehm
RisK-Design: Entwicklung von Risiko-Kompetenz im Stochastikunterricht. Eine Design-Based-Research Studie in der Sekundarstufe I
In ihrem Dissertationsprojekt beschäftigt sich Marie-Theres Brehm mit der Entwicklung von Risikokompetenz im Stochastikunterricht. Im Rahmen der design-basierten Forschungsstudie hat sie eine auf den Lebensweltbezug der Schüler*innen ausgerichtete Unterrichtsreihe zum daten- und konzeptbasierten statistischen Schließen im Bereich der Stochastik entwickelt, die mit verschiedenen Bremer Schulklassen in den Jahrgängen 9 und 10 erprobt wurde. Innerhalb der Unterrichtsreihe wird das Arbeiten, Auswerten und Interpretieren von Daten auf risikobezogene Fragen fokussiert. Dabei sollen empirisch basiert individuelle Vorstellungen von Risiko und Facetten von Risikokompetenz untersucht werden.
Das Projekt wird von Prof. Dr. Angelika Bikner-Ahsbahs betreut.
Luisa Gunia
Änderungen qualitativ denken – Argumentieren mit unterschiedlichen Sichtweisen auf den Funktions- und den Ableitungsbegriff
In ihrem Dissertationsprojekt beschäftigt sich Luisa Gunia mit dem vorstellungsorientierten und begrifflichen Argumentieren im Bereich qualitativer Analysis. Zu diesem Zweck hat sie eine auf das Verständnis der Schüler*innen hin ausgerichtete Unterrichtsreihe zum funktionalen Denken im Bereich der Analysis entwickelt und mit verschiedenen Bremer Schulklassen in der Einführungsphase erprobt. Innerhalb der Unterrichtsreihe werden verschiedene Perspektiven auf den Funktions- und den Ableitungsbegriff und das Zusammenspiel von Bestand und Änderung eröffnet. Es soll untersucht werden, welche Auswirkungen der Perspektivwechsel auf die von den Schüler*innen hervorgebrachten Argumente und Argumentationen hat und welche Vorstellungen vom Funktions- und vom Ableitungsbegriff dabei jeweils aktiviert werden.
Das Projekt wird von Prof. Dr. Christine Knipping betreut.
Martin Ohrndorf
Erklärvideos beeinflussen das Lernen von Funktionen!?
Martin Ohrndorf beschäftigt sich in seinem Dissertationsprojekt qualitativ und quantitativ mit der Analyse von Erklärvideos und deren Einfluss auf das Lernen von Funktionen. Zunächst untersuchte Martin qualitativ Erklärvideos von YouTube und Sofatutor auf drei verschiedene Angebotsarten: Angebote zur Herstellung von Geltung, Verstehensangebote und Beziehungsangebote. Basierend auf den Verstehensangeboten entstand in Zusammenarbeit mit Insa Meißner (Universität Bremen) ein Test zum konzeptuellen Wissen von Funktionen. Damit wurde in einem quasi-experimentellen Prä-Post-Design das Wissen von Schüler*innen des 8. und 9. Jahrgangs getestet. In einer ersten Kohorte wurde das Wissen in Abhängigkeit zur subjektiven Wahrnehmung des eigenen Wissens über Funktionen untersucht. In einer zweiten Kohorte wurde basierend auf den Beziehungsangeboten in Zusammenarbeit mit Vanessa Gross (Universität Bremen) das Wissen in Abhängigkeit zur parasozialen Beziehung ausgehend von den Videos und zur Matheangst untersucht.
Darüber hinaus arbeitet Martin in Zusammenarbeit mit Sina Wetzel (Universität Frankfurt am Main), Matthias Knippers (Universität Bielefeld), Julia Marie Stechemesser (Universität Duisburg-Essen), Juliane Wefers (Universität Bielefeld) und Lia Brüggemeyer (Universität Dortmund) an einer systematischen Literaturanalyse. Mit dieser Literaturanalyse möchten sie die Frage beantworten, inwiefern verschiedene Definitionen von mathematischen Erklärvideos in der Literatur vorkommen und auf welche hintergründigen Theorien diese Definitionen beruhen.
Das Projekt wird in Zusammenarbeit mit Prof. Dr. Florian Schmidt-Borcherding von Prof. Dr. Maike Vollstedt betreut.
Begutachtete Tagungs- und Zeitschriftenbeiträge sind mit einem Stern (*) gekennzeichnet.
* Ohrndorf, M., Meißner, I., Schmidt-Borcherding, F. & Vollstedt, M. (angenommen). Reconstruction of opportunities to understand the function concept from online explainer videos. Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13). Budapest, Ungarn.
Ohrndorf, M., Vollstedt, M., & Schmidt-Borcherding, F. (2023). Rekonstruktion von Angeboten zur Herstellung von Geltung in Erklärvideos zu Funktionen – (Wie) geht das? Beiträge Zum Mathematikunterricht 2022
, 1073-1076. Frankfurt a. M., Deutschland: 56. Jahrestagung der Gesellschaft für Didaktik der Mathematik. doi.org/10.17877/DE290R-23389
Ohrndorf, M. (2021). Verstehen verstehen. Eine Pilotstudie zur Überprüfung der Eye-Mind-Hypothese bei multimedialen Lernprozessen von Funktionen
. WTM-Verlag Münster. doi.org/10.37626/GA9783959873000.0
| 16.03.2022 | Rekonstruktion von Angeboten zur Herstellung von Geltung in mathematischen Erklärvideos: (Wie) geht das? | 28. Kongress der Deutschen Gesellschaft für Erziehungswissenschaft (DGfE-Kongress 2022) digital |
| 31.08.2022 | Rekonstruktion von Angeboten zur Herstellung von Geltung in mathematischen Erklärvideos: (Wie) geht das? | 56. Jahrestagung der Gesellschaft für Didaktik der Mathematik (GDM-Tagung 2022) an der Goethe-Universität Frankfurt, Deutschland |
| 11.07.2023 | Reconstruction of opportunities to understand the function concept from online explainer videos | 13th Congress of the European Society for Research in Mathematics Education (CERME13) an der Eötvös Loránd University (ELTE) am Alfréd Rényi Institute of Mathematics in Budapest, Ungarn |
| 18.09.2023 | Lernen mit Erklärvideos: Der Einfluss von Verstehensangeboten auf das Verstehen mathematischer Funktionen | 19. Fachgruppentagung Pädagogische Psychologie (PAEPS) an der Christian-Albrechts-Universität zu Kiel (CAU) am Leibniz-Institut für die Pädagogik der Naturwissenschaften und Mathematik (IPN) in Kiel, Deutschland |
Daniela Schansker
Von den natürlichen Zahlen zu den Dezimalbrüchen im dezimalen Stellenwertsystem: Ein Entwicklungsforschungsprojekt zur strukturfokussierenden Einführung der Dezimalbrüche mit der digitalen Stellenwerttafel
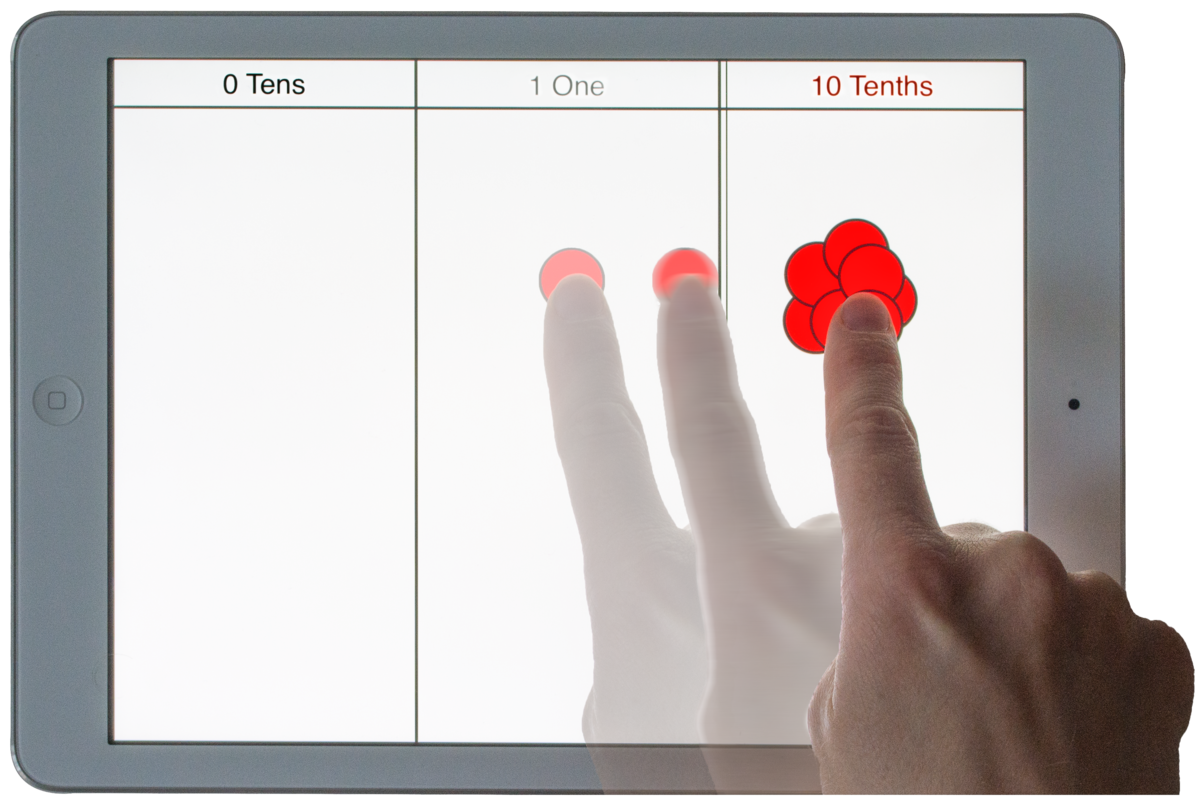
In ihrem Promotionsprojekt untersucht DanielaSchansker, wie eine digitale Stellenwerttafel auf dem iPad genutzt werden kann, um das dezimale Stellenwertsystem von den natürlichen Zahlen auf Dezimalbrüche zu erweitern.
Das Projekt wird von Prof. Dr. Angelika Bikner-Ahsbahs betreut.
Begutachtete Tagungs- und Journalbeiträge sind mit einem Stern (*) gekennzeichnet. Bis zum Jahr 2017 habe ich unter meinem Geburtsnamen Behrens publiziert.
Bikner-Ahsbahs, A., Burgarth, S., & Schansker, D. (2018). Komplementäres Scaffolding: digital und haptisch. In Fachgruppe Didaktik der Mathematik der Universität Paderborn (Hrsg.), Beiträge zum Mathematikunterricht 2018 (S. 285–288). Münster: WTM-Verlag.
Behrens, D., & Bikner-Ahsbahs, A. (2017). Indexikalität von Zeichen als Erklärungsansatz für epistemische Prozesse mit der digitalen Stellenwerttafel. In U. Kortenkamp & A. Kuzle (Hrsg.), Beiträge zum Mathematikunterricht 2017 (S. 67–70). Münster: WTM-Verlag.
* Behrens, D., & Bikner-Ahsbahs, A. (2017). The perspective of indexicality: How tool-based actions and gestures contribute to concept-building. In T. Dooley & G. Gueudet (Hrsg.). Proceedings of the 10th Congress of the European Society for Research in Mathematics Education (CERME10, 2017, S. 2721–2728). Dublin, Irland: DCU Institute of Education and ERME.
Behrens, D., & Bikner-Ahsbahs, A. (2016). Die digitale Stellenwerttafel: Aufgabendesign zur Einführung der Dezimalbrüche. In Institut für Mathematik und Informatik der Pädagogischen Hochschule Heidelberg (Hrsg.), Beiträge zum Mathematikunterricht 2016 (S. 117–120). Münster: WTM-Verlag.
* Behrens, D. & Bikner-Ahsbahs, A. (2016). The dragging gesture – from acting to conceptualizing. In C. Scíkos, A. Rausch & J. Szitányi (Hrsg.), Proceedings of the 40th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, S. 67–74). Szeged, Ungarn: PME.
* Behrens, D. (2015). How a digital place value chart could foster substantial understanding of the decimal place value system. In K. Krainer & N. Vondrová (Hrsg.), Proceedings of the 9th Congress of the European Society for Research in Mathematics Education (S. 2467-2472). Prag, Tschechische Republik: ERME.
Aylin Thomaneck
Vorgehensweisen bei der Interpretation kontextueller Graphen – eine Eye-Tracking Studie
In ihrem Promotionsprojekt untersucht Aylin Thomaneck mithilfe von Blickbewegungsmessungen (Eye-Tracking), wie Schüler*innen kontextuelle Graphen – also Graphen, deren Daten aus einem Realkontext stammen – interpretieren. Hierzu hat sie zunächst eine methodologische Fallstudie durchgeführt, in der untersucht wurde, wie Blickbewegungen bei der Interpretation kontextueller Graphen interpretiert werden können, inwieweit sie mit den kognitiven Prozessen der Lernenden während der Aufgabenbearbeitung übereinstimmen und welchen Beitrag Eye-Tracking in dieser Subdomäne leisten kann. Diese Erkenntnisse nutzt sie nun für empirische Studien zu Vorgehensweisen von Schüler*innen bei Interpretationsprozessen mit unterschiedlichen Anforderungen. Im Fokus stehen dabei insbesondere die Erfassung des Änderungsverhaltens kontextueller Graphen sowie die Zuordnung eines passenden realistischen Bildes zu einem kontextuellen Graphen, bei der häufig der sogenannte Graph-als-Bild-Fehler auftritt.
Das Projekt wird von Prof. Dr. Maike Vollstedt betreut.
Begutachtete Tagungs- und Zeitschriftenbeiträge sind mit einem Stern (*) gekennzeichnet.
* Thomaneck, A., Vollstedt, M., & Schindler, M. (angenommen). Matching a graph with an image representing the situational context: Students‘ approaches identified by using eye tracking. Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13). Budapest, Ungarn.
Thomaneck, A., Vollstedt, M., & Schindler, M. (2023). Eye-Tracking und Stimulated Recall Interviews zur Strategieanalyse bei der Erfassung der Änderung von Graphen. Beiträge zum Mathematikunterricht 2023, 1273-1276. Frankfurt a. M., Deutschland: Jahrestagung GDM. doi: 10.17877/DE290R-23277
* Thomaneck, A., Vollstedt, M., & Schindler, M. (2022). What can eye movements tell about students’ interpretations of contextual graphs? A methodological study on the use of the eye-mind hypothesis in the domain of functions.Frontiers in Education, 7. doi: 10.3389/feduc.2022.1003740
* Thomaneck, A., Vollstedt, M., & Schindler, M. (2021). Students‘ perception of change in graphs: an eye-tracking study.Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12), 1-11. Bozen-Bolzano, Italien: CERME 12.
* Thomaneck, A., Vollstedt, M., & Schindler, M. (2021). Students‘ perception of change in graphs: an eye-tracking study.Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education, Vol. 1, 184. Khon Kaen, Thailand: PME.
Thomaneck, A., Schindler, M., & Vollstedt, M. (2020). Kognitive Prozesse bei der Erfassung funktionaler Zusammenhänge: eine Eye-Tracking Studie.Beiträge zum Mathematikunterricht 2020, 1487. Würzburg, Deutschland: Jahrestagung GDM. doi: 10.17877/DE290R-21590
Abgeschlossene Promotionsprojekte
Dr. Estela A. Vallejo-Vargas (2023)
Titel der Dissertation: Learning to Teach Through Proving: In-service Primary School Teachers’ Understanding and Use of Proving while engaged in Proof-Based Teaching
Betreut von Prof. Dr. David Reid
Dr. Fiene Bredow (2023)
Titel der Dissertation: Mathematisches Argumentieren im Übergang von der Arithmetik zur Algebra. Eine qualitative Studie von Lehrkrafthandlungen im Mathematikunterricht
Betreut von Prof. Dr. Christine Knipping
Dr. Erik Hanke (2022)
Titel der Dissertation: Aspects and images of complex path integrals. An epistemological analysis and a reconstruction of experts' interpretations of integration in complex analysis
Betreut von Prof. Dr. Marc Keßeböhmer
Dr. Neruja Suriakumaran (2022)
Titel der Dissertation: Understanding the conceptual interplay between learners’ motivation and patterns of personal meaning in the mathematics classroom: results from Germany and Finland
Betreut von Prof. Dr. Maike Vollstedt & Prof. Dr. Markku Hannula
Dr. Nele Abels (2021)
Titel der Dissertation: Argumentation und Metakognition bei geometrischen Beweisen und Beweisprozessen. Eine Untersuchung von Studierenden des Grundschullehramts
Betreut von Prof. Dr. Christine Knipping
Dr. Chrysi Papadaki (2021)
Titel der Dissertation: The interconnective relationship of students’ visualization and argumentation in geometry
Betreut von Prof. Dr. Christine Knipping & Prof. Dr. David A. Reid
Dr. Jenny Cramer (2017)
Titel der Dissertation: Mathematisches Argumentieren als Diskurs. Eine theoretische und empirische Betrachtung diskursiver Hindernisse
Betreut von Prof. Dr. Christine Knipping
Dr. Thomas Janßen (2016)
Titel der Dissertation: Ausbildung algebraischen Struktursinns im Klassenunterricht: Lernbezogene Neudeutung eines mathematikdidaktischen Begriffs
Betreut von Prof. Dr. Angelika Bikner-Ahsbahs
Dr. Christina Krause (2015)
Titel der Dissertation: The Mathematics in Our Hands. How Gestures Contribute to Constructing Mathematical Knowledge
Betreut von Prof. Dr. Angelika Bikner-Ahsbahs
Dr. Thomas Bardy (2015)
Titel der Dissertation: Zur Herstellung von Geltung mathematischen Wissens im Mathematikunterricht
Betreut von Prof. Dr. Angelika Bikner-Ahsbahs

