Konsistente Approximationen der dreidimensionalen linearen Elastizitätstheorie
Thema:
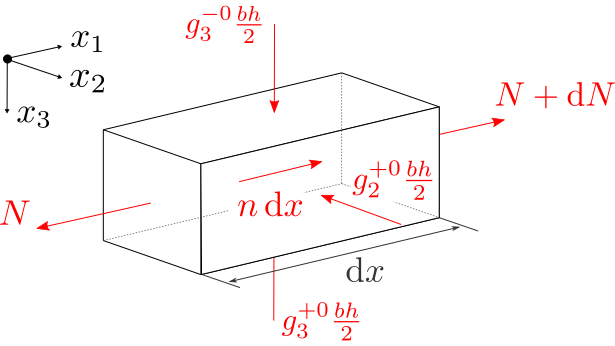
Zur Berechnung von Tragwerken (z. B. Träger, Stützen), die aus linear-elastischen Materialien (z. B. Metall, Keramik) bestehen, wird die 3D lineare Elastizitätstheorie verwendet. Diese Theorie lässt sich durch gekoppelte, partielle Differentialgleichungen darstellen und ist nur für wenige Sonderfälle geschlossen lösbar. Eine Vielzahl an geschlossen Lösungen ergeben sich durch 2D- und 1D-Approximationen. Der 2D-Fall enthält für gerade Strukturen das Platten- und Scheiben-Problem. Im 1D-Fall werden für gerade Strukturen zwei Balkenprobleme, ein Stab- und ein Wellen-Problem identifiziert.
Kontaktperson:
Laufzeit:
01.09.2015 - 31.08.2020
Partner:
Fachgebiet Konstruktiver Leichtbau und Bauweisen (KLuB), TU Darmstadt
Beschreibung:
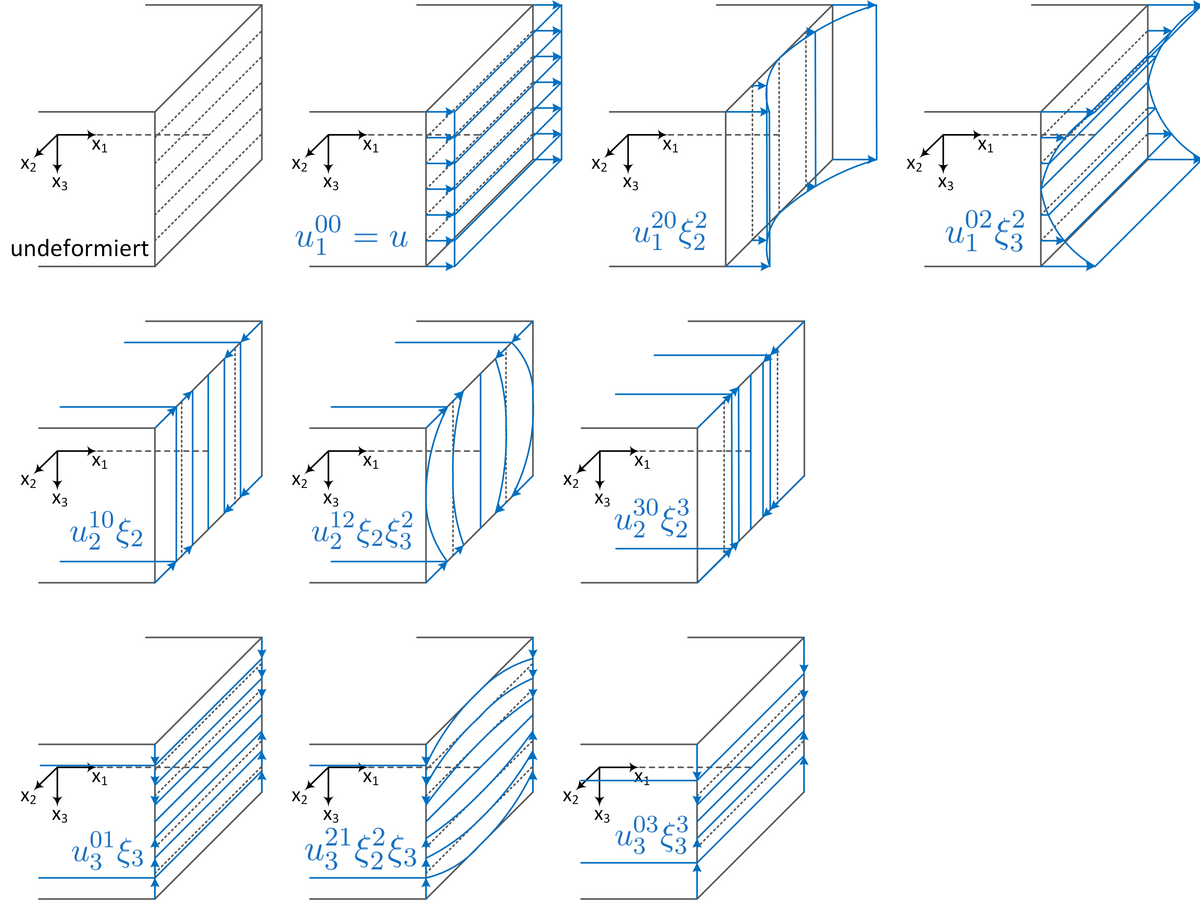
Klassischerweise werden sowohl 2D- als auch 1D-Theorien über kinematische a-priori Annahmen (vgl. Bernoullische Annahmen) hergeleitet. Basierend auf dem konsistenten Approximations-Ansatz, kommt das hier dargestellte Forschungsvorhaben ohne diese Annahmen aus. Bei diesem Verfahren werden nämlich die elastischen Potentiale der 3D-Theorie mit Reihenentwicklungen auf quasi 2D- bzw. 1D-Theorien reduziert. Die Äquivalenz zwischen diesen unendlichen Gleichungen und der 3D-Theorie konnte bereits nachgewiesen werden. Über den gleichmäßigen Approximations-Ansatz (Zerlegung über geometrische Kennzahlen) werden schließlich die unendlichen Gleichungen in lösbare Gleichungssysteme überführt.
Ein Hauptaugenmerk der Forschung liegt auf der Plattentheorie. Hier sollen zunächst die sogenannten "Reissner"-Terme (Randeffekte) mit in die konsistente Theorie eingebunden werden. Des Weiteren wird ein Verfahren entwickelt, um für alle Verschiebungskoeffizienten eine Differentialgleichung abzuleiten. Darüber hinaus sollen mit diesen Differentialgleichungen die lokalen Bedingungen erfüllt werden. Schließlich werden noch Plattentheorien mit verschiedenen Materialsymmetrien untersucht.
