TorchPhysics - A deep learning library for differential equations
Differential equations have to be solved in a wide variety of applications, usually by means of numerical simulations. Classical methods such as the Finite Element Method have shown to be succesful in various problems. However, some differential equations are very difficult to solve with classical methods, for example due to nonlinearities or their multi-scale character.
In recent years, a variety of upcoming deep learning approaches aimed to solve or simplify these issues.
Some of these approaches use neural networks to find a continuous representation of the solution function. The algorithms cover the determination of strong or weak solution as well as learning the differential operator itself and solving parameter identification or inverse problems.
While many applications of these approaches can be found in the literature, they often focus on specific problems and are implemented in different environments. Therefore, the aim of this project is to create a software package that combines various deep learning approaches for usage in various applications and further research. We therefore focus on an intuitive, flexible and modular code structure.
TorchPhysics is a Python library based on the deep learning framework PyTorch.
Currently, TorchPhysics can be used to:
- solve ordinary and partial differential equations
- learn parameter dependencies of solutions
- solve inverse problems
using algorithms from three different approaches.
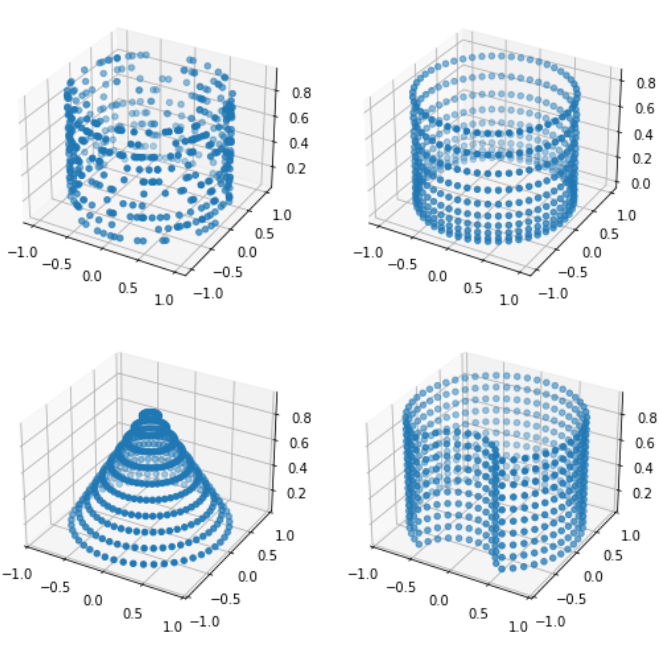
A special focus is placed on the flexible and efficient creation of points in easy-to-construct equation domains. To this aim, a set of methods for construction and import of domains are supplied. Implemented point samplers then act on these domains and their boundaries to create points following a variety of possible distributions, as they are necessary in all implemented DL-PDE methods. This basic building block forms a solid basis for the continuous extension of TorchPhysics.
The project is developed in cooperation with the Robert Bosch GmbH.
Link to the library: https://torchphysics.readthedocs.io/en/latest/index.html
Link to GitHub: https://github.com/boschresearch/torchphysics