Mapping local interaction forces by AFM
Introduction
The AFM combines a very sharp sensor, which can be positioned in all three dimensions with an accuracy of order Ångstrøm, with an ultrasensitive force sensor with a sensitivity on the order 10pN. This leads automatically to application, where either interaction forces are measured or minute forces are applied to the sample to investigate the response of the sample. The former has been applied to measure colloidal forces (1), the latter to measure specific binding forces (2), the elasticity (3) and force-response of single molecules (4) or the mechanical properties of soft samples (5). When combining force measurements and positioning the tip laterally on the sample interaction forces can be mapped locally (6), which has been applied to measure local electrostatic interactions (7) or local mechanical properties of living cells (8).
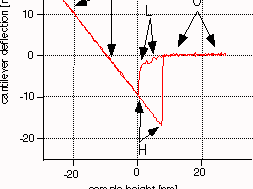
Force-Distance Curves
Force-Distance Curves or for short "force curves" are the basic mode of operation for measuring interaction forces with the AFM. In a force curve the deflection of the cantilever is measured while the z-height of the sample is ramped such that the tip gets into contact and out of contact again. Thus we distinguish the approach and retract part of force curves. On a stiff sample two major regimes can be distinguished: (1) if the tip is not touching the sample yet, the deflection stays constant and the force curve is flat and (2) in physical contact the deflection is proportional to the sample height, the force curve has a slope of unity. In addition two more features can be present. If there is adhesion between the tip and the sample a hysteresis during retract will be visible. The amount of hysteresis can be used to estimate the adhesion force between tip and sample. Under some circumstances long range force between tip and sample can occur before contact. Examples are magnetic or electrostatic forces. All these features are depicted in our example force curve in figure 1.
Colloidal Forces
In AFM all forces known from colloidal physics can be present. Always present are van der Waals forces, which are in most cases attractive and on the order 0.5 nN, depending on tip and sample material and geometry. When operated in air under ambient conditions the most prominent force will be the capillary force due condensation of a thin water layer which occurs on virtually any material. Typical values of this adhesion force for a hydrophilic material like glass or mica are larger than 10 nN. Thus detection of or operation at low forces is possible only in liquid environ ment (or under UHV conditions after appropriate sample preparation). In liquid, especially aque ous environment additional forces can be present: electrostatic interactions described by the Debye -Hückel theory of diffuse double layers, steric forces (e.g. with crafted polymer layers), chemical forces with functionalized surfaces, elastic forces with soft samples, and others. Here we will focus on elastic forces particularly in the context of living cells.
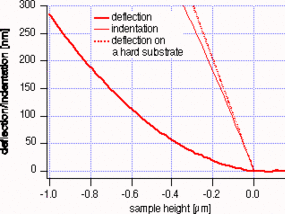
Nanomechanics of cells
On a soft sample such as a cell the force curve looks different than the one presented in figure 1 which has been taken on a stiff sample. In contact the tip will not directly follow the movement of the sample, because it intends the sample somewhat. It turns out that the curve will be non-linear in fact. The difference between a linear force curve taken on a stiff sample and a curved force curve taken on a soft sample will be the sample indentation. By modelling the geometry and material properties of the sample and the tip, we can calculate the local elastic or Young's modulus. The most simple model is the so called Hertz-model (9) in its extension by Sneddon (10) which is approriate in many cases, but fails to analyze the data under some circumstances. Cases in which the Hertz model fails are very thin parts of the sample such that the underlying stiff substrate is "felt" by the indenting AFM tip (11) or highly structured sample areas such as stress fibres in cells (12).

Elasticity map of a cell. By taking 64 * 64 force curves while raster scanning over the cell surface and subse-quently analyzing each individual force curve the local elastic or Young's modu lus has been obtained. This quantity has then been encoded in grey shades to yield the elasticity map presented here. Local differences in the elastic modulus due to cytoskeletal structures are appa-rent in this image.
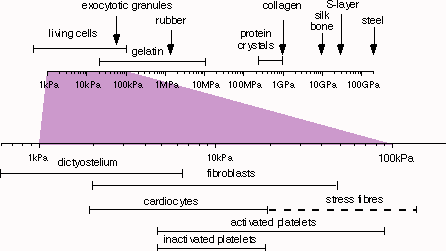
Young's moduli of different materials. The graph covers the range from hard materials used in engineering like steel (200 GPa), some stiff biological materials like a very special case of a bacterial cell wall (S-layer), silk and bone, plastic materials and finally cells at the lower end of the scale. Therefore, cells are by far the softest material compared to other materials known from daily experience, biological materials as well as man made.
Outlook
Force mapping mode has succesfully been applied to several questions on the mechanics of cells. We have reported on changes in cellular mechanics when applying substances degrading certain components of the cytoskeleton (13) or fixatives crosslinking cellular components (14) and during migration of active cells (15). Also, the mechanical properties of intact bacteria could be determined (16). Current projects extend the force mapping mode such that frequency dependent viscoelastic properties can be determined (17).

