Benchmark applications
The aquired concepts are evaluated mathematically and numerically in selected benchmark applications. This has a particular focus on scientific computing which incorporates expert information and serve as a basis for comparison with existing solutions in the applied sciences. Each research area has an assigned benchmark application.

Inverse scattering
Methods based on light scattering offer an inexpensive and efficient approach to testing the integrity of modern optical structures such as beam splitters or solar cells. This is a typical application where linearised models for light scattering processes do not yield satisfactory results. To obtain sufficiently precise solutions, the underlying wave propagation problem has to be modelled by Maxwell's equations, leading to a non-linear and ill-posed inverse scattering problem. Although a substantial amount of results on inverse scattering from bounded objects has been obtained during the last 30 years, identifying parameters of surface structures and, in general, three-dimensional electromagnetic inverse scattering problems still present challenging problems due to their huge complexity when it comes to numerical computations. Even more, for aperiodic surfaces, the well-developed theory on scattering from periodic structures does not apply, such that, for Maxwell’s equations, there are already quite few results on the well-posedness of the forward problem. To reduce the complexity of solution algorithms, methods aiming to determine crucial features of a searched-for parameter rather than the parameter itself recently received much interest in inverse scattering, for instance by determining directly the interior eigenvalues of some scattering object instead of the object itself, or by computing merely the support of a scatter by a sampling method instead of characterising its properties in terms of coefficients explicitly. The attempt to construct such methods is part of a broader trend to try to directly solve for features instead of the unknown parameter itself, which is both stabler and faster in contrast to first determining the parameter and then extracting the critical feature.
As a result of the 1st cohort for this benchmark application we highlight the simulation and reconstruction experiments of Thies Gerken for the case of time-dependent parameters. In this case the underlying hyperbolic PDEs cannot simply be reformulated as a Helmholtz equation. Thies Gerken developed a theory as well as a software for simulations. In particular analysed the acoustic wave equation, and the related inverse problems of reconstructing a time- and space-dependent wave speed and mass density from the solution of this equation.
Magnetic Particle Imaging
Magnetic particle imaging (MPI) is a relatively new imaging modality. The nonlinear magnetization behavior of nanoparticles in an applied magnetic field is exploited to reconstruct an image of the concentration of nanoparticles. The first comercialy sold scanner (UKE Hamburg-Eppendorf) and the applied field are illustrated in the following: Finding a sufficiently accurate model to reflect the behavior of large numbers of particles for MPI remains an open problem.
As such, reconstruction is still computed using a measured forward operator obtained in a time-consuming calibration process. The model commonly used to illustrate the imaging methodology and obtain first model-based reconstructions relies on substantial model simplifications. One needs to take into account the magnetization dynamics of the nanoparticles' magnetic moment (red) such as Brownian (left) and Neel rotation (right) into the direction of the applied field (green). By neglecting particle-particle interactions, the forward operator can be expressed by a Fredholm integral operator of the first kind which yields the the inverse problem for image reconstruction. First results on this benchmark application include a concept for superresolution reconstructions (see T. Kluth, C. Bathke, M. Jiang, P. Maaß: Joint super-resolution image reconstruction and parameter identification in imaging operator: Analysis of bilinear operator equations, numerical solution, and application to magnetic particle imaging, 2020). The application of a CNN (3D autoencoder) to 3D MPI reconstructions has been introduced by Sören Dittmer (Deep image prior for 3D MPI: A quantitative comparison of different regularization techniques on Open MPI dataset, submitted).
Domain Walls
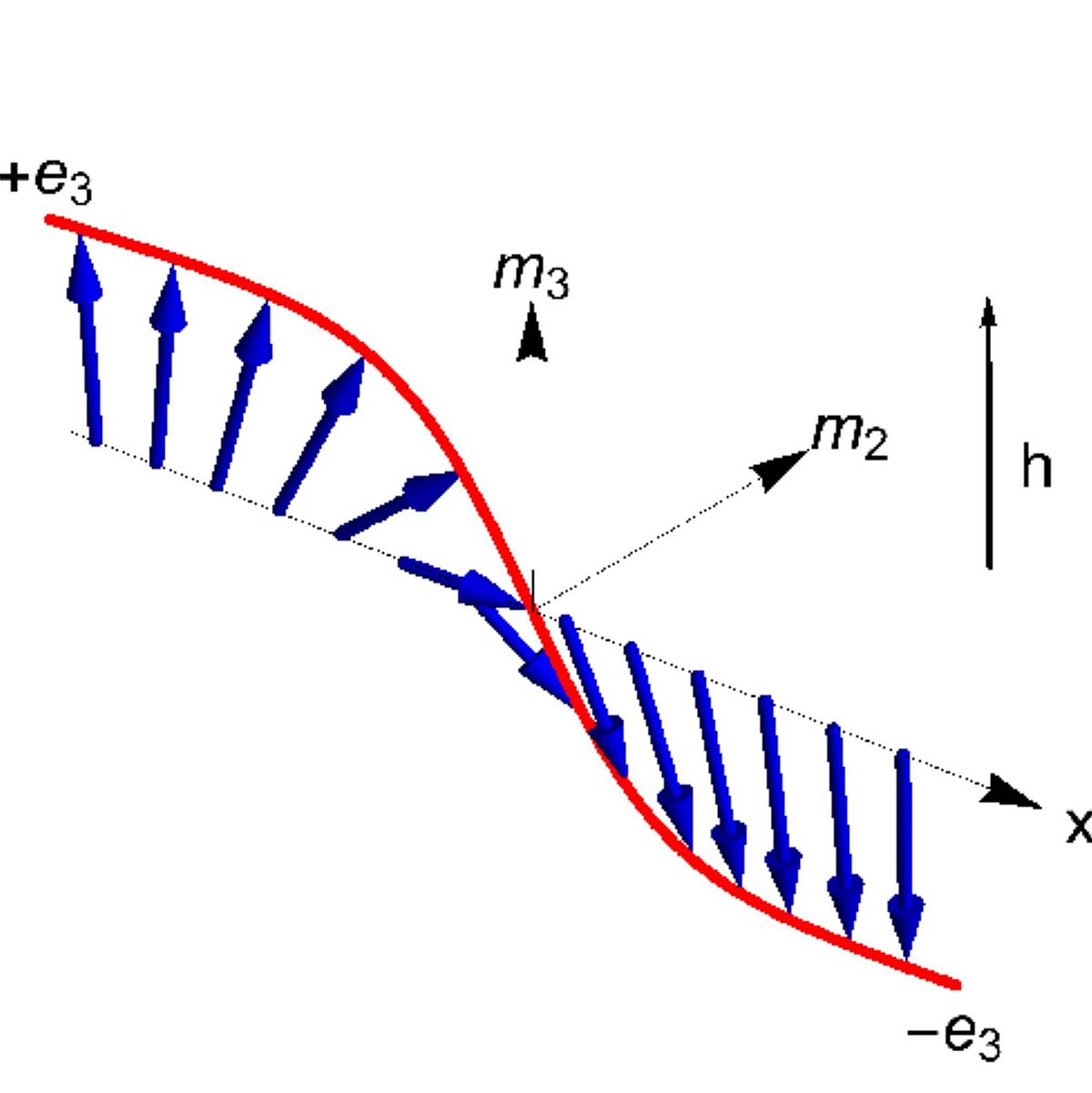
Spintronic nanowires have been suggested as a technology for data storage devices based on domain walls that separate regions of different magnetisation. Decisive for the theoretical underpinning is an understanding of the existence and dynamical properties of domain walls, as well as control of their motion and locations in the nanowire. Opposing pairs of domain walls encode a 1-bit that should reliably be read out or generated by controlling the locations of domain walls. The mathematical study concerns idealised partial differential equation models that are based on extensions of the Landau-Lifschitz equations. First results obtained within the RTG concern additional results on the existence of domain walls, their characteristic velocity and frequency, as well as the stability properties of single domain walls (see L. Siemer, I. Ovsyannikov, J.D.M. Rademacher: Inhomogeneous domain walls in spintronic nanowires, 2020).
Automotive
The benchmark application is centered around the area of autonomous driving of passenger cars. A test vehicle (VW Passat GTE Plug-in-Hybrid) is available, which is approved to drive on Bremen's roads for research purposes. The car has been adapted in order to access the standard sensor (camera, ultrasound) and actuator technology. Furthermore, it is equipped with additional sensors (camera, lidar) to obtain various information about its environment. A GNSS module supported by a Real-Time Kinematic (RTK) system allows for high precision localization. This is necessary for the automatic control framework, but can also be used for data recordings (for an overview see OPA3L). The application offers a variety of facets to be used within this research area, such as parameter identification for the ODE model, optimal control, object detection, or sensitivity-based controller updates. Nonlinear dynamics and real-time requirements make the application challenging.
MALDI Imaging
MALDI (matrix assisted laser desorption and ionization) mass spectrometry is an analytic method for the identification of proteins, metabolites, lipids and other compounds and macromolecules within biological tissue samples (Nobel prize Koichi Tanaka, 2003). In MALDI imaging, introduced in 2005, this technology is applied in a spatially resolved manner, allowing to investigate the complete metabolic and proteomic landscape of a sample. By imaging a stack of consecutive tissue sections, the method can be extended to 3D. The vast amount of information contained in a single MALDI imaging dataset (data size 2 - 100 GB) poses severe challenges to the data analysis methods. Dimensionality reduction and feature extraction aim at identifying relevant features within the dataset, possibly utilizing application specific a-priori information and training data. Methods include conventional peak picking as well as numerical matrix factorization methods, data clustering and neural networks. Supervised machine learning methods are used to develop classification models for specific applications (e.g. tumor typing and grading). High prediction accuracies can be achieved based on adaptive designs of experiments and clinical trials.
Highlights obtained by the PhD students of the 1st cohort include an application of learned models to digital pathology (see J. Behrmann, C. Etmann, T. Boskamp, R. Casadonte, J. Kriegsmann, P. Maaß: Deep Learning for Tumor Classification in Imaging Mass Spectrometry, 2018). As well as the adaptation of a theoretical paper (see P. Fernsel, P. Maaß: A Survey on Surrogate Approaches to Non-negative Matrix Factorization, 2018) to MALDI imaging data (see J. Leuschner, M. Schmidt, P. Fernsel, D. Lachmund, T. Boskamp, P. Maaß: Supervised Non-negative Matrix Factorization Methods for MALDI Imaging Applications, 2018).
Learning Algorithms
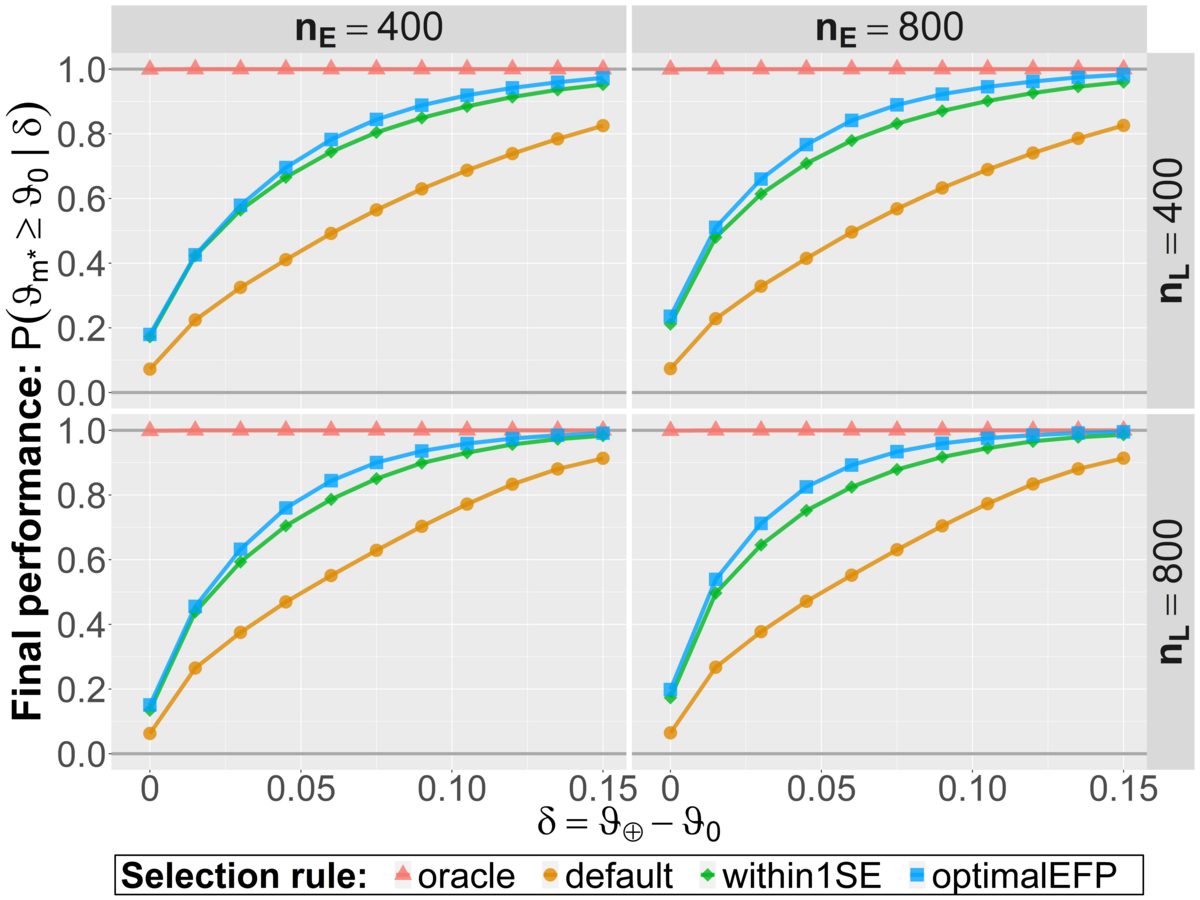
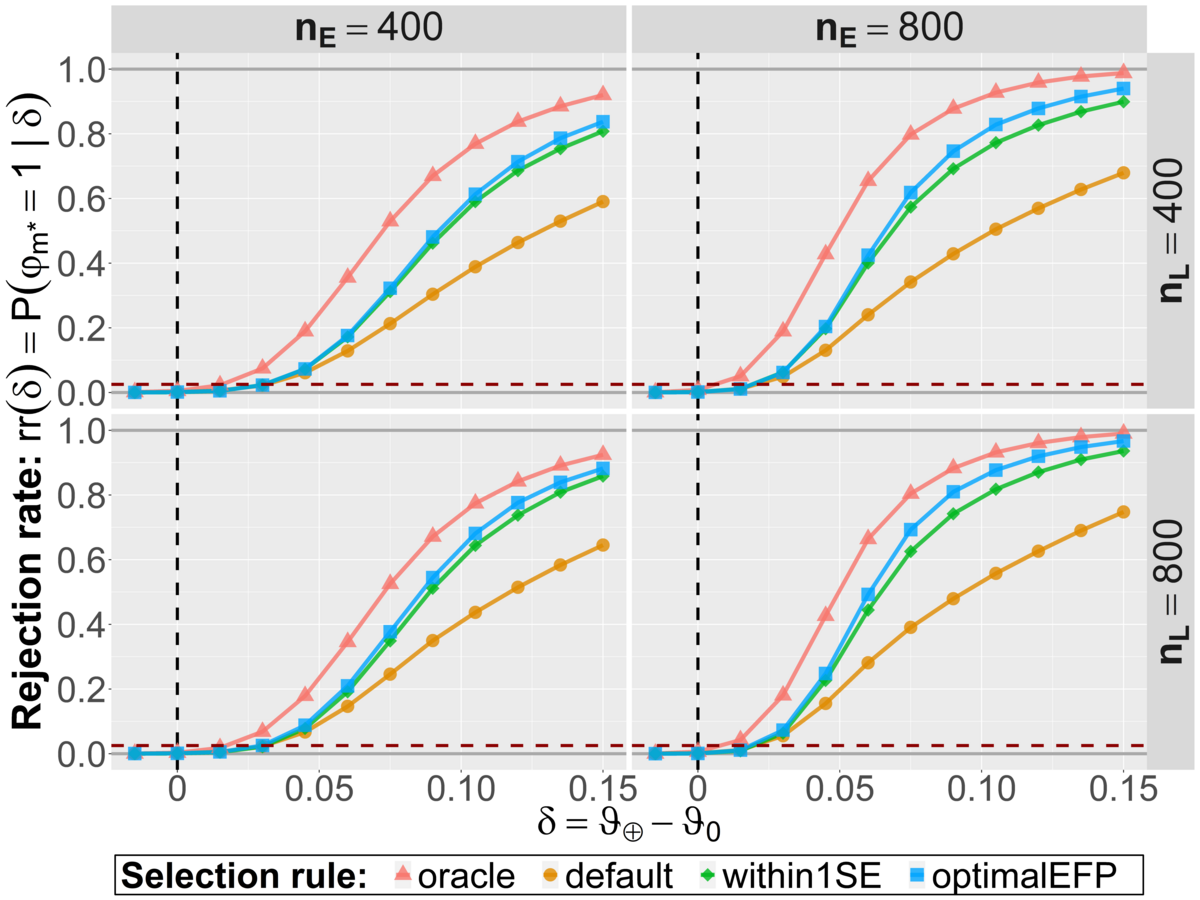
Research project R3-4 involves several numerical simulation studies with the overall goal to compare different model evaluation strategies. The general idea of these numerical experiments is to simulate the whole process of machine learning and evaluation many thousand times in different realistic scenarios. Hereby we have used popular machine learning algorithms to train between 40 and 200 initial candidate models for binary classification tasks. The numerical implementation of the optimal EFP selection rule is based on a simulation of the evaluation study ahead and informed by the (validation) data already observed. Hereby, parameter values are simulated from a generative distribution which is obtained as the posterior distribution based on preliminary data from the model development phase. The relevant evaluation data is then sampled from the parameter-dependent (likelihood) model. Together, this allows to simulate the final selection process in the evaluation study. In our numerical experiments, all relevant operating characteristics were improved with this novel rule compared to the heuristic within 1 SE approach. For the most part, the additional benefit was however not too pronounced. The default approach to evaluate a single model on the test data performs worse regarding the final model performance and statistical power as illustrated in the two figures below (M. Westphal, A. Zapf and W. Brannath: A multiple testing framework for diagnostic accuracy studies with co-primary endpoints, 2020).