R3: Data analysis
Research area R3 analyses data-driven approaches, which are complementary to the model-based approaches of research areas R1 and R2. Such data driven approaches have seen increasing research activities over the last decade, particularly in the fields of machine learning (model, basis learning) and topological data analysis with astonishing applications in fields such as genomics and bioinformatics. Data-driven approaches are also starting to be applied in order to improve model-based parameter identification tasks, e.g. feature reconstruction or adjusting model inconsistencies in direct optimisation. At the core of data-driven approaches to parameter identification are the classical problems of feature extraction, clustering, and classification.
Deep learning
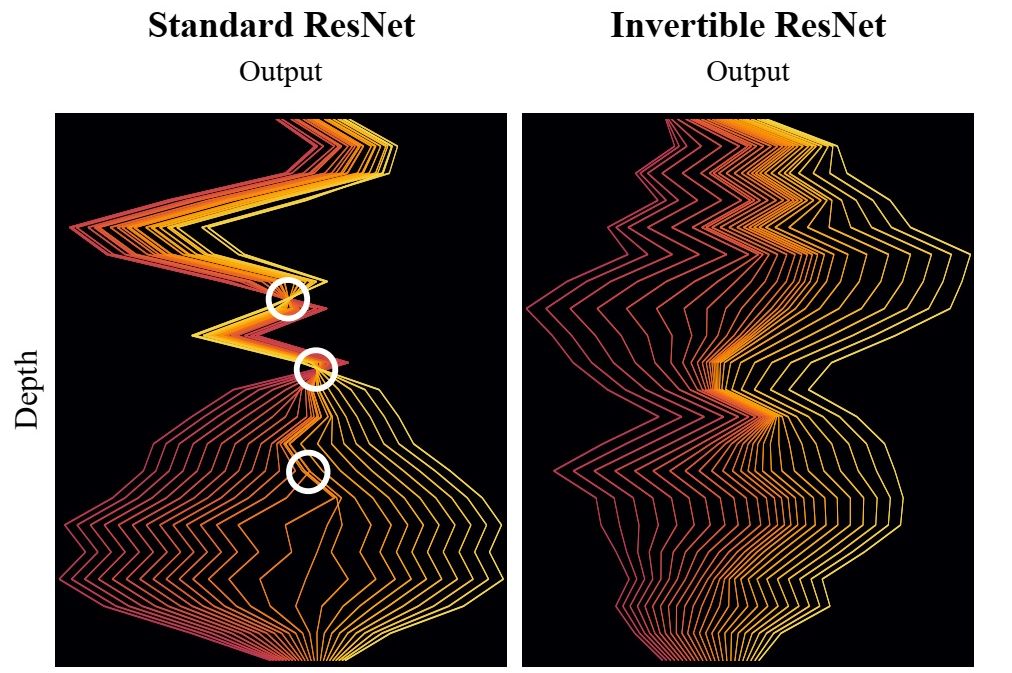
During the first years deep learning (DL) has become a major research topic in R3. Here the aim is to embed the striking, but experimental results using deep neural networks into a stringent mathematical theory. The emphasis is on applying DL concepts to inverse problems. For first theoretical results see (S. Dittmer, T. Kluth, P. Maaß, D. Otero Baguer: Regularization by architecture: A deep prior approach for inverse problems, 2020 and C. Etmann, S. Lunz, P. Maaß, C. Schönlieb: On the Connection Between Adversarial Robustness and Saliency Map Interpretability, 2019).
The 2nd cohort of PhD students of R3 continues to strengthen the statistical side of data analysis with two PhD students working on post-selection Inference for Prediction Performance (Pascal Rink) and on statistical hypotheses testing and interval estimation for prediction performance (Vladimir Vutov).
Also, we do have two PhD students (Lena Ranke, Gideon Klaila) who are investigating concepts of topological data analysis and its theoretical foundations. This is a new research direction of our RTG with a high-potential of collaborations with the PhD projects working on the benchmark applications but also to Research Area R2.
Furthermore we continue our work on mathematical foundations of deep learning where several PhD students (Maximilian Schmidt, Hannes Albers, Johannes Leuschner, Jean Le'Clerc Arrastia, Jose Carlos Gutierrez Perez) are working on theoretical as well as applied topics related to digital pathology and tomography.


Optimal model selection
As part of research area 3 in the 1st cohort, the task of optimal model selection in supervised machine learning was addressed in PhD project R3-4. Data splitting is essential to separate model development and selection on the one hand and model evaluation on the other hand. However, the frequently recommended strict evaluation of only a single final model which must be selected before based on independent data is quite inflexible. Therefore, the main goal of this research project was to utilize the test data for model selection by employing a subset selection rule in conjunction with an adjusted final analysis on the test data. A novel subset selection rule which was derived in the framework of Bayesian decision theory was proposed. The general goal of this optimal EFP selection rule to maximize the posterior expected utility, the expected final performance, based on the current state of knowledge. The main innovation was the hereby employed utility function which is independent of the subset size. This is an advantage to other approaches because the procedure has no additional hyperparameters to be determined by the practitioner. Moreover, the so-called maxT-approach to the simultaneous assessment of sensitivity and specificity as co-primary endpoints for multiple binary classifiers was adapted. This extends the default evaluation strategy in confirmatory (phase III) diagnostic test accuracy studies where usually only a single candidate model is assessed. The co-primary endpoint analysis is the standard approach in such studies as overall accuracy alone is rarely sufficient to adequately capture the performance of a classifier for medical testing applications. The new procedure asymptotically controls the FWER in the strong sense. For finite sample sizes, this approach is too liberal under least-favourable parameter configurations, in particular when many models are compared against baseline values close to one. However, in realistic scenarios in the machine-learning context, the FWER was always controlled regardless of the employed selection rule in our numerical experiments (see M. Westphal, W. Brannath: Improving Model Selection by Employing the Test Data, 2019 and M. Westphal, A. Zapf, W. Brannath: A multiple testing framework for diagnostic accuracy studies with co-primary endpoints, 2019).
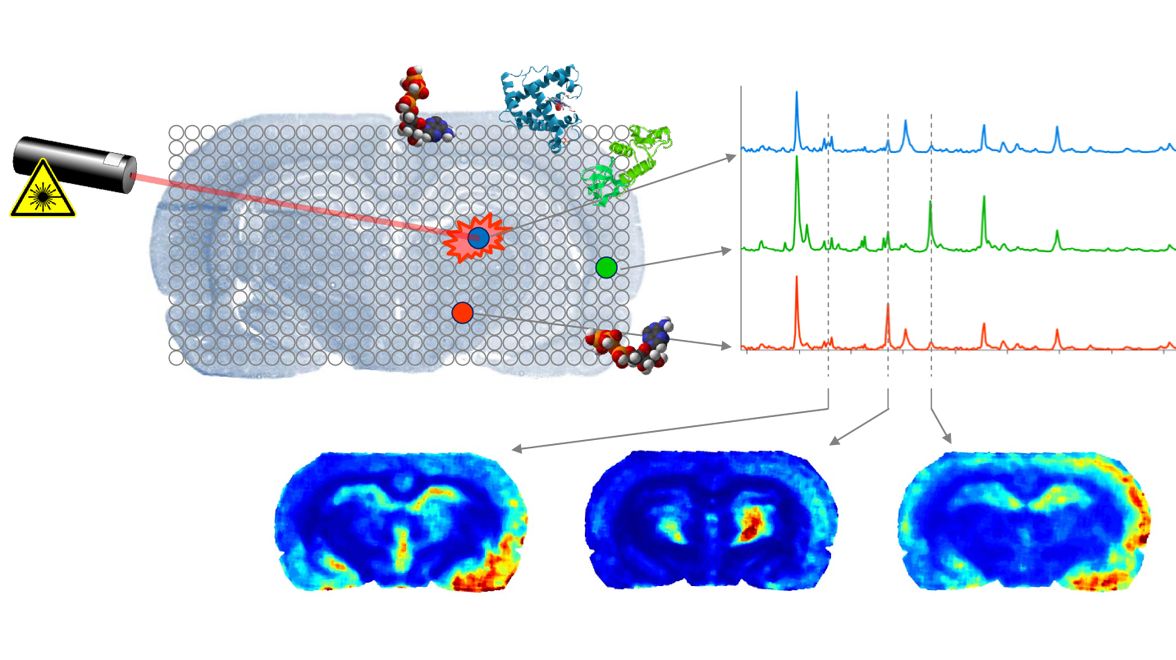
These concepts were successfully applied to testing different neural network designs for clustering of MALDI data and subsequent classification tasks in digital pathology. For further results on analyzing hyperspectral MALDI data see the benchmark application.

