R2: Direct optimisation
A paradigm of applied science is to create so-called digital twins of real systems - a task naturally in the class of parameter identification problems that can be found in numerous engineering areas, e.g. aeronautics, automotive, or maritime applications.
In order to achieve this goal, this RTG research area deals with the application of finite-dimensional nonlinear programming theory and mathematical analysis to problems involving infinite-dimensional components – ordinary or partial differential equations – and also to systems involving large data sets and highly advanced models. Herein direct optimisation avoids the use of dual optimality theory in the original problem formulation by the direct numerical solution of first-order optimality criteria and/or the transcription of optimal control problems into large and sparse nonlinear optimisation problems (following the concept of “first discretise, then optimise”). On the one hand, this relies on the numerical solution using adequate methods, for which a deep understanding of the underlying algorithms is essential. On the other hand, we develop mathematical methods for a refined analysis of the model equations and their direct control. For practical applications, not only the mere solution of optimisation problems is of interest, but also other requirements such as parametric sensitivity, stability, and industrial demands. In this research area, the focus is on the analysis of these aspects and the development of efficient algorithmic implementation of both innovative mathematical methods and combinations of existing approaches.
Highlights
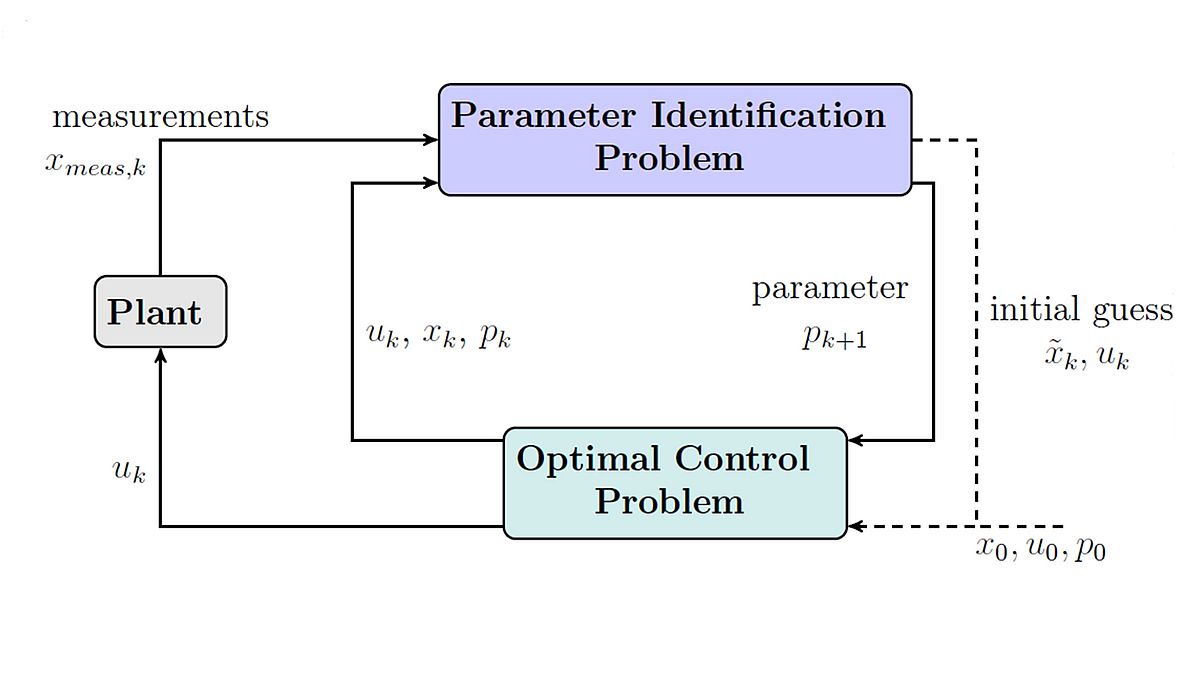
The 1st cohort of PhD students focused on parameter identification problems mostly involving ordinary differential equations. On the one hand, algorithms for online updates of time-dependent model parameters during system execution and a combination of a real-time adapted Riccati controller with online parameter identification is investigated. On the other hand, decomposition techniques as multiple shooting are investigated with respect to finding desired solutions. This is all accompanied by a robotic benchmark application.
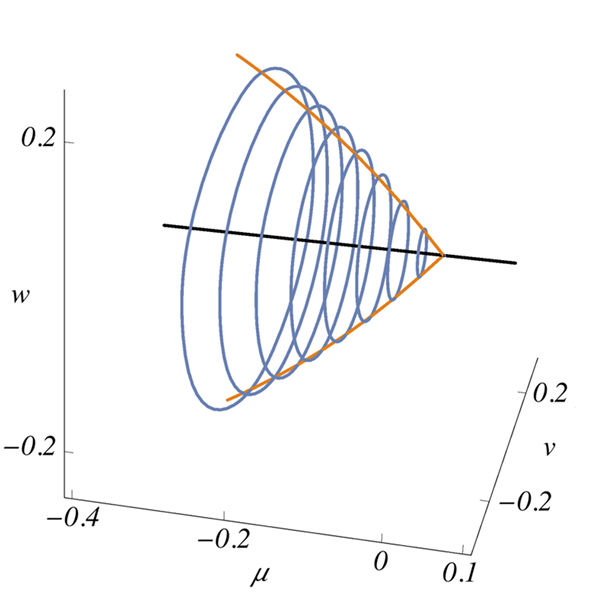
Another highlight in this research area is the identification of a safety parameter for a bifurcation, which appears in periodic solutions of an ordinary differential equation with a non-smooth nonlinearity. It represents the motion of a ship (the “Hamburg test case”), for which it is rigorously proven that a yaw-damping and yaw-restoring control is always safe.
The 2nd cohort builds on these results by the aim to classify several local minima as being preferable and considering the convergence to these. Moreover, structure identification and machine learning approaches are added to the portfolio of R2 with autonomous driving as benchmark application. In addition, the integration and analysis of models for magnetisation is considered towards the second phase of the RTG.