Discrete Lorenz attractor
(Prof. Dr. Jens Rademacher)
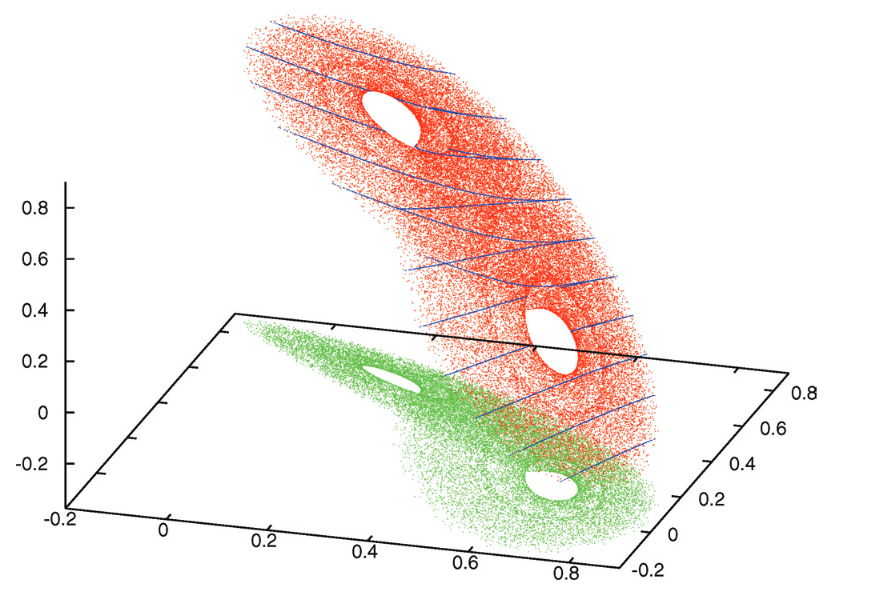
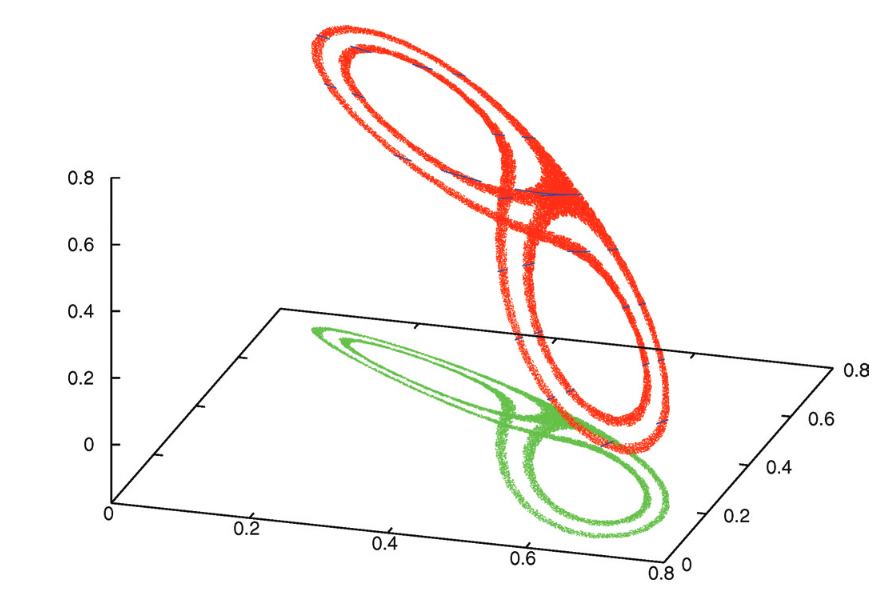
The discrete Lorenz attractor (DLA) is a recently discovered chaotic object (see image below). Its form is similar to that of the classical (continuous) Lorenz attractor and provides another example of robust chaotics - the DLA and its chaotic properties are preserved under small perturbations (for example, external forces, noise, etc.). In papers [1] and [2], a class of discrete systems in which a DLA exists was presented. In this project, the question of whether such a DLA can also exist in inverse mapping will be investigated analytically as well as numerically. This project takes place in collaboration with Dr. I. Ovsyannikov from the University of Hamburg.
Basic knowledge of calculus as well as linear algebra is recommended and basic knowledge of numerics would be advantageous. The duration of the work within the working group should be at least four weeks. In addition, a written paper and a final presentation in the seminar are expected. Further information and requirements can be found in the module and event catalog of the Department of Mathematics.
A written presentation of this project can be found here.