Dynamical Systems with Substitutions 1
(Prof. Dr. Anke Pohl)
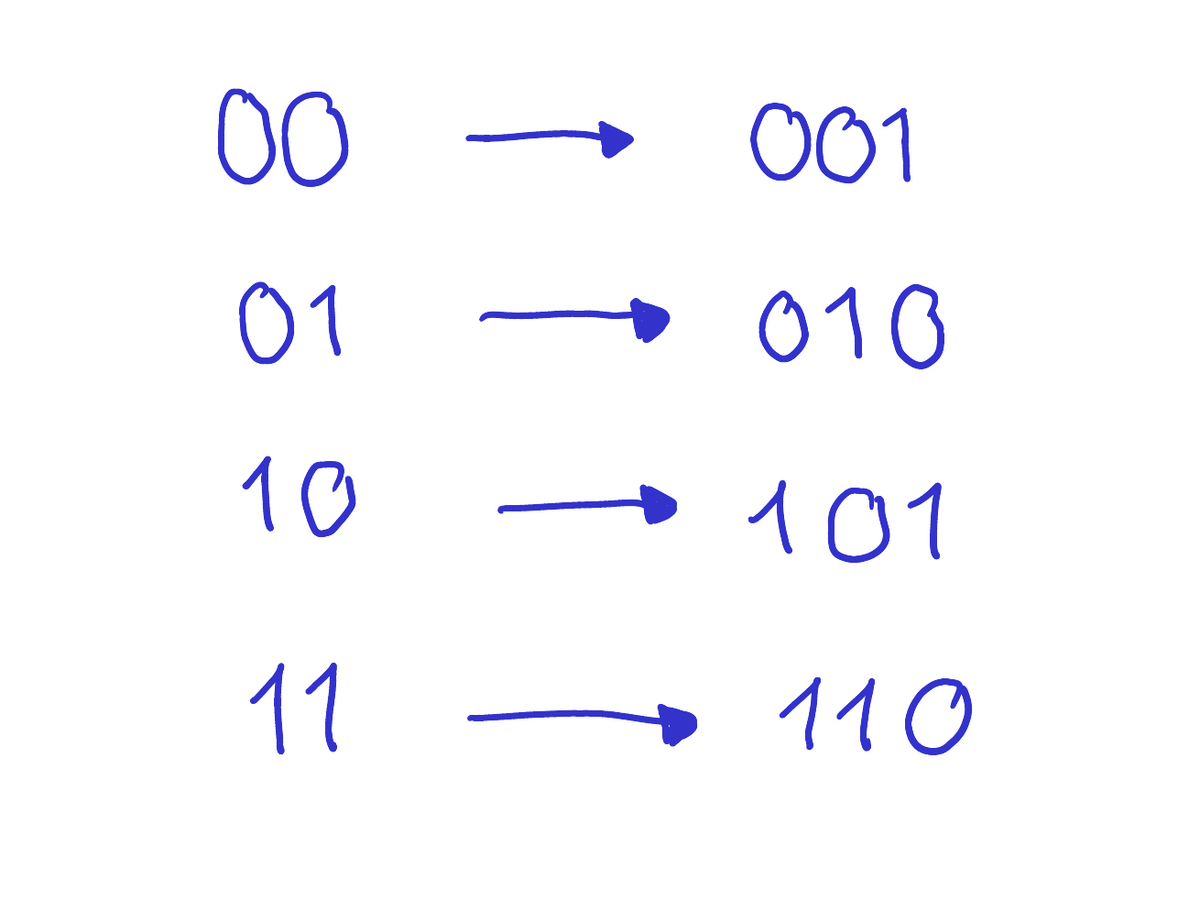
In many situations, dynamical systems occur naturally, which can be described by substitutions. Such dynamical systems consist of a set of infinite sequences over an alphabet and dynamics given by iterative substitution of selected finite sequences of letters by other sequences of letters. A prominent example is Conway's game of life. In this project, we study the dynamical substitution system for infinite sequences over the two-letter alphabet {0,1}, where the substitution is given as shown below (see figure below).
Basic knowledge of calculus and linear algebra is recommended, as well as some programming knowledge. The duration of the work within the working group should be at least four weeks. In addition, both a written and an oral final presentation in the seminar are expected.
