Mathematiker*innen im Beruf
Mathematik und Finanzwelt
Die Mathematik und das Risiko

Mit Chancen und Risiken beschäftigt sich jeder von uns täglich. Nehme ich den Regenschirm mit, oder gehe ich das Risiko ein komplett durchnässt an meinem Zielort anzukommen? Finanzkrisen haben gezeigt, dass auch Banken sich nicht nur mit ihren Chancen, sondern auch mit ihren Risiken beschäftigen müssen. Und genau hier kommt die Mathematik ins Spiel. Sie hilft bei der Modellierung von schwankenden Marktpreisen, um möglichen hohen Verlusten vorzubeugen. Sie hilft aber auch bei der Modellierung von möglichen Krisen, in dem sie Auswirkungen von Lieferengpässen oder politischen Umstürzen abbildet. Das Anwendungsfeld von Mathematik ist sehr breit bei Banken und reicht von einfachen statistischen Modellen bis hin zu Machine Learning.

Dr. Anna-Lena Martins studierte Mathematik an der Georg-August Universität Göttingen und hat 2019 in der angewandten Mathematik promoviert. Seitdem ist sie bei KPMG tätig und hat sich sowohl in der Beratung als auch im Bereich der Jahresabschlussprüfung mit Risikomanagementsystemen von Banken und anderen Finanzdienstleistern beschäftigt. Aktuell unterstützt sie bei Bankengründungen und begleitet u.a. Unternehmen aus der Finanztechnologie bei dem Aufbau von neuen Instituten hinsichtlich Risikomanagementthemen. Sie begeistert vor allem die Themenvielfalt der Branche.
Mathematik, Finanzwelt und Management
Die Aufgaben von Banken sind unter anderem die Organisation des Zahlungsverkehrs und die Vermittlung zwischen Geldanbietern und Geldnachfragern, also zwischen Sparern und Kreditnehmern.
Eine wichtige Aufgabe, bei der Mathematik eine große Rolle spielt, ist z.B. die Verschlüsselung des Zahlungsverkehrs.
Weitere wichtige Fragen sind: Wie viel Kredite können innerhalb eines Jahres ausfallen? Wie viel Geld kann innerhalb eines Tages abgebucht werden? Wie viel kostet es uns, wenn die Zinsen plötzlich steigen?
Auch die Digitalisierung erfordert immer mehr mathematische Fähigkeiten. Die Kundenkommunikation mit Texterkennung (Chatbots) oder Spracherkennung setzt mathematische Modelle voraus, die Automatisierung von Arbeitsabläufen die Entwicklung von Algorithmen.
Banken lassen sich ohne anspruchsvolle mathematische Systeme gar nicht mehr steuern. Mathematiker sind in der Lage zu verstehen, was da genau passiert. Sie haben die Fähigkeit diese Systeme zu beherrschen und nicht von ihnen beherrscht zu werden.

Dr. Tim Nesemann studierte Mathematik in Bremen und promovierte in Bremen und an der University of Rhode Island, USA. Anschließend absolvierte er ein Studium zum Diplom-Kaufmann. Seit 1995 ist er bei der Sparkasse Bremen tätig. Zunächst im Kundengeschäft, seit 2004 als Mitglied des Vorstandes der Sparkasse Bremen mit Verantwortung u.a. für Finanzen, Risiko, Kreditüberwachung und IT. Seit Dezember 2007 als stellvertretender Vorstandsvorsitzender, seit 1. Februar 2009 als Vorsitzender des Vorstandes.
Mathematik und Raumfahrt
Mathematik in der Raumfahrt

Wir schauen uns die Grundlagen der Bilddatenauswertung von Raumsonden an. Wie entsteht das dreidimensionale Modell eines kleinen Himmelskörpers wie beispielsweise des Saturnmondes Mimas aus Kameradaten während des Vorbeifluges der Raumsonden Cassini und Voyager? Hierzu bedarf es einiger mathematischer Kniffe und Rechenschritte, die uns auch auf der Erde bei 3D- Scannern helfen, Formen zu erkennen. Zudem: Was können wir aus der Flugbahn einer Raumsonde, die dicht an einem solchen Körper vorbeifliegt, über das Innere des Körpers lernen?

Dr. Marco Scharringhausen studierte 2000 - 2003 Mathematik in Oldenburg und Osnabrück und war im Anschluss im Institut für Umweltphysik an der Uni Bremen tätig. Seit 2007 ist er raumfahrtbegeisterter Mitarbeiter des Deutschen Zentrums für Luft- und Raumfahrt am Institut für Raumfahrtsysteme in Bremen und beschäftigt sich dort mit der Erkundung der Planeten und anderer Körper in unserem Sonnensystem in der Abteilung Lande- und Explorationstechnologie.
Mathematik in der Raumfahrt
Wir schauen uns die Grundlagen der Bilddatenauswertung von Raumsonden an. Wie entsteht das dreidimensionale Modell eines kleinen Himmelskörpers wie beispielsweise des Saturnmondes Mimas aus Kameradaten während des Vorbeifluges der Raumsonden Cassini und Voyager? Hierzu bedarf es einiger mathematischer Kniffe und Rechenschritte, die uns auch auf der Erde bei 3D-Scannern helfen, Formen zu erkennen.
Zudem: Was können wir aus der Flugbahn einer Raumsonde, die dicht an einem solchen Körper vorbeifliegt, über das Innere des Körpers lernen? Wir werden sehen, dass wir ohne Zuhilfenahme weiterer Instrumente schon eine Menge über den inneren Aufbau aussagen können.

Dr. Jörg Klatte studierte Technomathematik an der Universität Bayreuth. Seine Promotion hat er im Anschluss am Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation (ZARM) an der Universität Bremen im Bereich Flüssigkeitsdynamik in der Schwerelosigkeit absolviert. Seit 2011 arbeitet er als Experte für Flüssigkeitsdynamik bei der Ariane Group in Bremen an der Weiterentwicklung zukünftiger Raumfahrtsysteme.
Materialwissenschaften in Schwerelosigkeit

Materialwissenschaftler beschäftigen sich mit den Zusammenhängen zwischen Herstellung, Struktur und Eigenschaften von Materialien, oft mit dem Ziel Werkstoffe mit neuen oder verbesserten Eigenschaften zu (er)finden. Am Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation (ZARM) gibt es seit 2016 eine Arbeitsgruppe, die untersucht, wie sich die Herstellung in Schwerelosigkeit auf Materialeigenschaften auswirken kann. Dabei liegt das Hauptaugenmerk auf der Steigerung der Energieeffizienz der Materialien. Mathematische Modelle, welche die Eigenschaften in Abhängigkeit von der Struktur vorhersagen, können hierbei richtungsweisend sein und die Anzahl der nötigen Experimente stark verringern.

Magdalena Thode studierte (angewandte) Mathematik und Physik an der Universität Bremen und in den Niederlanden. Seit 2016 arbeitet und promoviert sie am Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation (ZARM). Sie erforscht dort, inwieweit Eigenschaften der Elektrolumineszenz von Zink-Sulfid-Materialien durch die Herstellung in Schwerelosigkeit verbessert werden können.
Mathematik und Medizin
Statistische Modellierung von Gesundheitsdaten

Gesetzliche Krankenkassen erheben Daten zu Abrechnungszwecken. Nebenbei sind diese Daten aber auch eine wertvolle Datenquelle für die Gesundheitsforschung. Der Umfang der Daten macht es z.B möglich, Studien zu seltenen Nebenwirkungen von Arzneimitteln im Alltagsgebrauch durchzuführen. Die statistischen Modelle und Schätzverfahren in diesen Studien müssen dabei viel leisten: Sie müssen auf das spezifische Design jeder Studie angepasst werden und gut interpretierbare, korrekte und möglichst präzise Schätzungen hervorbringen. Aufgrund der enormen Datenmenge sind effiziente Algorithmen zur Schätzung ebenfalls notwendig. Die Mathematik dient dabei als Fundament, um Verfahren mit diesen Eigenschaften zu entwickeln oder bestehende Modelle zu verbessern.

Dr. Dirk Enders hat an der Universität Bremen Mathematik studiert und im Anschluss am BIPS in Bremen in Statistik promoviert. Seit 2018 arbeitet er in Berlin am InGef – Institut für angewandte Gesundheitsforschung und leitet dort das Team Biometrie & Data Science. Sowohl während seiner Promotion als auch in Berlin widmete er sich intensiv der Analyse von Abrechnungsdaten der gesetzlichen Krankenkassen. Er schätzt besonders das interdisziplinäre Arbeiten in den Studien mit Experten aus den Bereichen Gesundheitswissenschaften, Medizin, Statistik und Informatik.
Mathematik und medizinische Bilder
Wir sind längst im Zeitalter der digitalen Medizin angekommen. Medizinische Daten und Bilder, welche mit modernen physikalischen Methoden erfasst werden, haben einen so hohen Informationsgehalt, dass mathematische Modellierung und Simulation einen erheblichen Mehrwert beitragen. Von der Optimierung der Erfassung, der Aufbereitung der Daten, der Simulation der physiologischen Prozesse, bis zur Optimierung der Therapie, ist die angewandte Mathematik ein Grundpfeiler der modernen Medizin. Hier ist die Arbeit eines Mathematikers nah an den Schnittstellen zu anderen Fachbereichen, oft zu Physik, Medizin, Informatik und Biologie.

Dr. Cristoffer Cordes arbeitet am Fraunhofer MEVIS als Forscher. Er hat an der Universität Bremen Mathematik studiert und seinen Master von der Clemson University (USA) verliehen bekommen. Danach hat er an der Universität Bremen in Physik promoviert. Sein Hauptfokus ist die MRT-Simulation und die abstrakte MRT-Sequenzentwicklung.
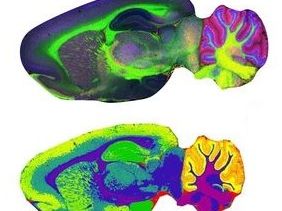
Mathematik in den Life Sciences
Die Technologie der bildgebenden Massenspektrometrie ermöglicht die örtliche Lokalisierung und Quantifizierung von Molekülen, wie beispielsweise Proteinen, Peptiden oder Wirkstoffen. Anwendungen findet die bildgebende Massenspektrometrie beispielsweise in der Pharmakologie zur Entwicklung neuer Medikamente und Wirkstoffe, in der medizinischen Forschung zur Erforschung neuer Therapien, in der Pathologie zur Detektion neuer krankheits-charakterisierender Biomarker und in den Materialwissenschaften zur Optimierung neuer Werkstoffe. Die riesigen Datenmengen der bildgebende Massenspektrometrie zu visualisieren, zu analysieren und zu interpretieren ist eine Herausforderung, die man mit Hilfe mathematischer Verfahren bewältigen kann.

Dr. Dennis Trede studierte Mathematik in Dresden und Bremen. Nach seinem Diplom 2007 promovierte er 2010 am Zentrum für Technomathematik der Universität Bremen im Bereich der Inversen Probleme. Seit 2010 ist er CEO des Startup SCiLS, das er zusammen mit Peter Maass und Theodore Alexandrov gegründet hat. Im Jahr 2015 wurde SCiLS mit dem Bremischen Gründerpreis ausgezeichnet und 2017 an Bruker verkauft. Seit 2019 ist Dennis Trede Direktor für Software Strategy and Business Development im Bereich Life Sciences Mass Spectrometry bei Bruker.
Industriemathematik

Mathematik in der Energie- und Telekommunikations- branche
In einem Versorgungsunternehmen ist es von entscheidender Bedeutung, große Datenmengen zu analysieren und zu verstehen, um den Betrieb zu optimieren und den Kunden den bestmöglichen Service zu bieten. Hierfür ist das Erstellen von Programmcode unerlässlich, was auf mathematischen Konzepten basiert. Mit der steigenden Bedeutung von KI-Anwendungen ist Mathematik als Grundlage für die Entwicklung von Algorithmen und Modellen ebenfalls unverzichtbar geworden. Darüber hinaus kann eine Grundausbildung in Mathematik dazu beitragen, ein strukturiertes Denken und eine logische Arbeitsweise zu fördern, was in einem komplexen und datenintensiven Arbeitsumfeld, wie dem der Energiebranche, von großem Vorteil ist.

Dr. Miriam Steinherr kommt aus Barcelona, Spanien und hat Mathematik an der Universitat Autònoma de Barcelona studiert. Ihren Master hat sie an derselben Universität absolviert und ist dann im Jahr 2017 nach Deutschland gezogen, um an der Universität Bremen zu promovieren. Nach ihrer Promotion hat sie als Postdoc an der Constructor University (früher Jacobs University) gearbeitet und seit 2023 ist sie bei EWE im Team Business Intelligence als Data Analyst tätig. Ihr Schwerpunkt liegt bei der Entwicklung von Datenmodellen, um die Informationen über Kunden, Produkte und alles, was damit zusammenhängt, besser zu verstehen sowie die Entwicklung von Prognosemodellen, um zukünftige Ereignisse frühzeitig und besser einschätzen zu können.

Windparkoptimierung: Mehr Ertrag durch intelligente Betriebsführung
Windturbinen erzeugen Energie über eine Lebensdauer von mehr als 20 Jahren. Sie sind so ausgelegt, dass in dieser Zeit die Belastungen unter verschiedensten Betriebsbedingungen in der Umwelt und vom elektrischen Netz standhalten. Außerdem müssen sie steigende und teils noch unbekannte Anforderungen des künftigen Energiesystems erfüllen. Um diese Anforderungen zu erfüllen, forschen wir an intelligenten Strategien zur Betriebsführung von einzelnen Anlagen und ganzen Windparks. Dabei legen wir besonderen Wert auf eine optimale Balance zwischen Energieertrag, lastabhängigem Lebensdauerverbrauch und langfristigem Wert. Dabei kommen verschiedenste mathematische Methoden von klassischer Regression und KI-Modellen über stochastische Vorhersagen bis zur nichtlinearen Optimierung zum Einsatz.

Niklas Requate hat sein Studium der Technomathematik an der Uni Bremen 2018 abgeschlossen und im Anschluss als wissenschaftlicher Mitarbeiter am Fraunhofer IWES angefangen. Dort betreibt er angewandte Forschung mit direktem Bezug zur Industrie. Er arbeitet an intelligenten Methoden zur Betriebsführung von Windenergiesystemen unter Berücksichtigung der Zuverlässigkeit. Dabei ist er begeistert von der Vielzahl an Themen, die dabei von Bedeutung sind. Für eine optimale Betriebsweise muss das Zusammenspiel aus stochastischen Einflüssen des Windes, mechanischer Belastung und wirtschaftlicher Bewertung betrachtet und bewertet werden.
Mathematischer Beitrag zur Stahlerzeugung

Bei der Stahlerzeugung sind viele Prozesse und Zwischenschritte erforderlich, bis das fertige Produkt schließlich zum Kunden kommt. An sehr vielen Stellen sorgt dabei Mathematik in verschiedensten Formen dafür, dass dies möglichst gut funktioniert. Man kann sogar so weit gehen zu sagen: Ohne Mathematik ist eine ökologische und effiziente Produktion von hochwertigem Stahl unmöglich. Dementsprechend beschäftigen sich im Stahlwerk von ArcelorMittal Bremen einige Mathematiker unter anderem mit der Entwicklung von Algorithmen zur Lösung komplexer Probleme, der Automatisierung und Digitalisierung mittels KI oder der Untersuchung von Prozessen dahinter.

Sven Koelmann studierte Technomathematik mit Anwendungsfach Produktionstechnik in Bremen. Während seines Studiums machte er verschiedene Praktika, unter anderem bei UNESP Bauru in Sao Paulo, Brasilien. Nach dem Abschluss seiner Masterarbeit in Zusammenarbeit mit ArcelorMittal Bremen arbeitet er seit 2015 als Modellexperte Operations Research bei ArcelorMittal und beschäftigt sich mit der Entwicklung und Anwendung von Algorithmen zur Automatisierung und Optimierung verschiedener Prozesse. Zur Zeit ist er Koordinator des Bereichs Operations Research in der Abteilung Modelle & Simulationen.
Mathematik und Quantencomputing

Quantencomputing – das auf der Quantenmechanik basiert – ist eine komplexe Technologie, die für die meisten Menschen schwer zu verstehen ist. Völlig neue Algorithmen – und sogar neues Denken – sind erforderlich, um das Potenzial der kommenden Quantencomputer auszuschöpfen. Dies erfordert neue Ansätze, um Quantencomputing auf ansprechende und verständliche Weise für IT-Experten, Entwickler und junge Akademiker zu vermitteln. Wir wollen neben den Grundlagen des Quantum Computing ansehen, wie man dieses Thema greifbar machen und möglichst allgemeinverständlich darstellen kann. Dazu werden "Serious Games for Quantum Computing" und ein funktionierendes Modell der IBM Quantum System One Quantencomputers genutzt.

Dr. Jan-Rainer Lahmann studierte Technomathematik an der TU Clausthal und hat 1999 am KIT Karlsruhe in angewandter Mathematik promoviert. Seitdem ist er in der IBM Deutschland in verschiedenen Positionen in der technischen Vertriebsunterstützung tätig. Seit einigen Jahren ist er begeistert von der gänzlich anderen Welt des Quantencomputing. Dr. Lahmann ist IBM Distinguished Engineer und Mitglied der IBM Academy of Technology.
Optimierung in der Stahlindustrie

Seit über 60 Jahren wird in Bremen Stahl produziert. Hochöfen und große industrielle Anlagen prägen das Bild im Bremer Norden an der Weser. Doch welche Rolle spielt Mathematik in einem Stahlwerk? Im Zuge der Digitalisierung werden immer mehr mathematische Modelle benötigt, zum Beispiel um Anlagen besser auszulasten oder Produktionskosten zu minimieren.

Insa Poppen studierte Technomathematik an der Universität Bremen. Nach der Masterarbeit, die sie in Zusammenarbeit mit Jacobs Kaffee erstellte, begann sie 2015 als Modellexpertin bei ArcelorMittal Bremen zu arbeiten. Als Mitglied der Abteilung Modelle und Simulation ist sie zuständig für mathematische Modelle im Bereich der Automatisierung.
Mathematik und Softwareentwicklung
Mathematik und Softwareentwicklung- Wo ist der gemeinsame Nenner?
Im Mathematikstudium wird einem beigebracht, systematisch an komplexe Probleme heranzugehen, komplizierte Aufgaben zu verstehen, zu analysieren und eine exakte Vorgehensweise zu gebrauchen. Softwareentwickler*innen sind zuständig für die Planung, Analyse, Entwicklung, Implementierung und Wartung von Anwendungen und Softwarebausteinen. Strukturiertes Denken ist somit eine essentielle Fähigkeit für die Softwareentwicklung.
Teelka Emkes hat 2017 ihren Master in Mathematik an der Universität Bremen abgeschlossen. Nach ihrer Masterarbeit hat sie sich autodidaktisch das Programmieren angeeignet und seit Juli 2018 arbeitet sie als Java Softwareentwicklerin bei Team Neusta. Bei ihrer Arbeit entwickelt sie die Sportwebseiten für verschiedene Vereine, wie zum Beispiel Werder Bremen.
KI - Fahrschule für Autonome Autos

Die menschliche Kompetenz, Auto zu fahren, basiert nicht nur auf dem erlernten Wissen aus der Fahrschule. Vor allem sind hier auch alle Fähigkeiten relevant, die im Laufe eines Lebens gelernt werden. Diese erlauben uns, Situationen einzuschätzen, Vorhersagen über das Verhalten anderer zu machen und so schließlich ein vorausschauendes Führen des Fahrzeuges - ohne besonders darüber nachzudenken! Doch wie erreicht eigentlich ein selbstfahrendes Auto diese Expertise? Wir widmen uns dieser Frage und werden dabei insbesondere feststellen, welch fundamentale Rolle die Mathematik bei ihrer Beantwortung einnimmt.
Autonome Raumschiffe, Agrarmaschinen und vor allem auch Autos - die Steuerung solcher Systeme steht im Zentrum der Forschung von Andreas Folkers. In den Jahren 2013 - 2018 absolvierte er ein Studium der Technomathematik an der Universität Bremen und arbeitet hier seither als wissenschaftlicher Mitarbeiter an aktuellen Fragestellungen in diesen Themengebieten. Im Fokus seines Promotionsvorhabens steht besonders die Entwicklung von Regelkonzepten und Künstlicher Intelligenz (KI).
Mathematik und Modellierung
Mathematik in der musikalischen Akustik

Mathematik und Musik scheinen nah und fern zugleich. Schon die Pythagoräer waren von der mathematischen Gesetzmäßigkeit der Musik überzeugt. Gleichzeitig spielt Mathematik im Leben vieler Musiker keine große Rolle. Möchte man jedoch die Entstehung und Wirkungsweise musikalischen Klangs verstehen, kommt man um Mathematik nicht herum. Diese liefert die richtigen Werkzeuge, um die Grundbausteine des Klangs zu beschreiben. Mit Hilfe mathematischer Modelle ist es möglich, Klänge wie mit einer Art akustischen Skalpell zu zerlegen, zu manipulieren, und auch wieder zusammenzusetzen. Damit ist es der Forschung im Bereich der Akustik möglich, einen Bogen zu spannen, der die mathematische Beschreibung des Klangs einerseits und die subjektive Wahrnehmung des Klangs andererseits verbindet.

Kai Siedenburg hat 2012 sein Studium der Mathematik mit dem Nebenfach Musikwissenschaft an der Humboldt Universität Berlin abgeschlossen. Anschließend promovierte er an der McGill University in Montreal zur Wahrnehmung von Musik. Seit 2016 arbeitet er im Department für medizinische Physik und Akustik an der Universität Oldenburg, wo er derzeit eine Arbeitsgruppe zum Thema der Musikwahrnehmung leitet. Sein Ziel ist es, die akustischen Grundlagen der Musik zu erforschen und damit zu einer Verbesserung von Hörhilfen beizutragen.
Was macht eine Mathematikerin in der Arktis?

Wir alle möchten gerne wissen, wie das Wetter wird, ob wir heute Abend grillen können oder nicht, ob nächstes Wochenende Freibad oder Spielenachmittag angesagt ist, usw. Und auch für das Klima würden wir gerne genauer wissen, wie es weitergeht, was macht der Klimawandel genau und was hat er für Auswirkungen? Für all diese Vorhersagen brauchen wir mathematische Modelle, mit deren Hilfe wir berechnen, wie sich das Wetter oder das Klima in der Zukunft entwickeln wird. Eine wichtige Rolle spielen dabei die Wolken, die nicht nur oft wunderschön am Himmel aussehen, sondern auch einen großen Einfluss haben und furchtbar kompliziert sind. Sie setzen sich aus winzigen Tröpfchen zusammen, können sich zu riesigen Gebilden aufbauen und werden von großen Strömungen beeinflusst. Viele Prozesse müssen wir auch noch besser verstehen, um sie anschließend in unseren Modellen besser abbilden zu können. Dafür beobachten und simulieren wir Wolken weltweit - zum Beispiel auch in der Arktis, die im Augenblick besonders sensibel auf den Klimawandel reagiert und sich stärker erwärmt als der Rest der Welt.

Dr. Vera Schemann hat 2009 ihr Studium der Technomathematik mit dem Nebenfach Geowissenschaften an der Universität Bremen abgeschlossen. Anschließend hat sie am Max-Planck-Institut für Meteorologie in Hamburg promoviert und dort angefangen sich mit der Modellierung von Wolken und ihrer Darstellung in Klimamodellen zu beschäftigen. Seit 2015 arbeitet sie am Institut für Geophysik und Meteorologie an der Universität zu Köln. Die Wolken haben sie nicht mehr losgelassen und so versucht sie noch immer diese besser zu verstehen und die entscheidenden Prozesse in mathematischen Modellen abzubilden





